8．如图，小明想测量电线杆AB的高度，发展电线杆的影子恰好落在土坡的坡面CD和地面BC上，量得CD=4米，BC=10米，CD与地面成30°角，且此时测得1米杆的影长为2米，则电线杆的高度约为_______米．(结果保留两位有效数字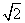，≈1.41，≈1.73)

7．四边形ABCD中，∠C=90°，AB=12，BC=4，CD=3，AD=13，则四边形ABCD的面积为________．

6．在直角三角形中，三个内角度数的比为1：2：3，若斜边为a，则两条直角边的和为________．

5．在△ABC中，∠C=90°，b=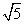，三角形面积为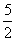，则斜边c=_____，∠A的度数是____．

4．为测一河两岸相对两电线杆A、B间距离，在距A点15m的C处，(AC⊥AB)，测得

∠ACB=50°，则A、B间的距离应为(　　 )m

　　 A．15sin50°　　 B．15cos50°　　 C．15tan50°　　 D．15cot50°

3．在△ABC中，∠C=90°，a，b，c分别是∠A，∠B，∠C的对边，有下列关系式：①b=ccosB，②b=atanB，③a=csinA，④a=bcotB，其中正确的有(　 )

　　 A．1个　　 B．2个　　 C．3个　　 D．4个

2．在△ABC中，∠C=90°，a=5，c=13，用科学计算器求∠A约等于(　 )

　　 A．24°38′　　 B．65°22′　　 C．67°23′　　 D．22°37′

1．在下面条件中不能解直角三角形的是(　 )

　　 A．已知两条边　　　 B．已知两锐角　　 C．已知一边一锐角　 D．已知三边

17.(1)证明:如答图,连结BI,

∵I为△ABC的内心,∴∠1=∠2,∠3=∠4,

∵∠5=∠1+∠3,∠2=∠6,∴∠5=∠4+∠6,

又∵∠EBI=∠4+∠6,

∴∠EBI=∠BIE,∴IE=BE.

　　 (2)解:∵∠1=∠2,∠2=∠6,∴∠1=∠6.

又∵∠E=∠E,∴△BDE∽△ABE,

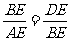∴ ,∴BE²=AE·DE,即IE²=DE·AE,

∵IE=4,AE=8,∴4²=8DE,∴DE=2.

更多资料请访问http://www.maths.name

16.证明:连结OD,∵OA=OD,∴∠1=∠2,

∵AD∥OC,∴∠1=∠3,∠2= ∠4,

∴∠3=∠4,

在△OBC和△ODC中,∵∠3=∠4, ,

∴△OBC∽△ODC,∴∠OBC=∠ODC,

∵BC是⊙O的切线,∴∠OBC=90°,

∴∠ODC=90°,∴DC是⊙O的切线.