4．已知圆锥的底面半径为2，母线长为5，则圆锥的侧面积为　　　　　 ，底面积为　　　　　 ．

3．半径为4，圆心角为90°的弧的长为　　　　　 ．

2．一个圆锥的侧面积是底面积的3倍，则这个圆锥的侧面展开图的圆心角是　　 度．

1．用一个面积为60cm²的长方形纸片围成一个圆柱，则这个圆柱的侧面积为　　　　　 cm²．

　习题3、4 　　　　　　　　　　　　　　　　　　　　　　

　　 例1、一个圆锥形零件的母线长为a，底面的半径为r，求这个圆锥形零件的侧面积和全面积．

　解　 圆锥的侧面展开后是一个扇形，该扇形的半径为a，扇形的弧长为2πr，所以

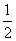　　　　S_侧＝×2πr×a＝πra；

　　　　　S_底＝πr²；

　　　　　S＝πra+πr²．

答：这个圆锥形零件的侧面积为πra，全面积为πra+πr²

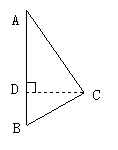
(难)例2、已知：在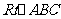中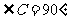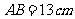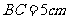，，，，求以AB为轴旋转一周所得到的几何体的全面积.

分析：以AB为轴旋转一周所得到的几何体是由公共底面的两个圆锥所组成的几何体，因此求全面积就是求两个圆锥的侧面积.

解：过C点作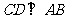，垂足为D点因为三角形ABC是，，，，

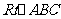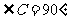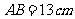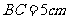所以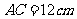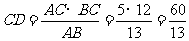底面周长为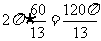

所以S_全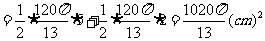

答：这个几何体的全面积为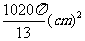　　　　　　　　　　

2.圆锥侧面展开图是扇形，这个扇形的半径与圆锥中的哪一条线段相等？

待学生思考后加以阐述.

圆锥的底面周长就是其侧面展开图扇形的弧长，圆锥的母线就是其侧面展开图扇形的半径.

圆锥的侧面积就是弧长为圆锥底面的周长、半径为圆锥的一条母线的长的扇形面积，而圆锥的全面积就是它的侧面积与它的底面积的和.

问题：圆锥的母线有几条？

　　　　 (二)实践与探索 ： 圆锥的侧面积和全面积的计算方法

　　 问题：

1.沿着圆锥的母线，把一个圆锥的侧面展开，得到一个扇形，　　 这个扇形的弧长与底面的周长有什么关系？

3、扇形的面积是S，它的半径是r，这个扇形的弧长是_____________

(三)应用与拓展

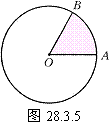
　　 例1如图28.3.5，圆心角为60°的扇形的半径为10厘米，求这个扇形的面积和周长．(π≈3.14)

例2、右图是某工件形状，圆弧BC的度数为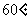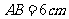，，点B到点C的距离等于AB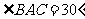，，求工件的面积.

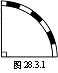　　 如图28.3.1是圆弧形状的铁轨示意图，其中铁轨的半径为100米，圆心角为90°．你能求出这段铁轨的长度吗?(取3.14)我们容易看出这段铁轨是圆周长的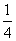，　 所以铁轨的长度 l≈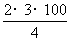＝157.0(米).

问题：上面求的是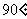的圆心角所对的弧长，若圆心角为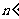，如何计算它所对的弧长呢？

请同学们计算半径为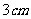，圆心角分别为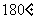、、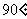、、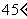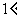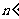所对的弧长.

等待同学们计算完毕，与同学们一起总结出弧长公式(这里关键是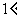圆心角所对的弧长是多少，进而求出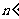的圆心角所对的弧长.)

弧长的计算公式为

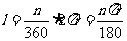
练习：已知圆弧的半径为50厘米，圆心角为60°，求此圆弧的长度.

(二)

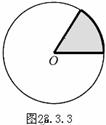
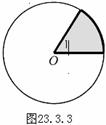
情境与探究2：扇形的面积.　　 如图28.3.3，由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形

问：右图中扇形有几个？

同求弧长的思维一样，要求扇形的面积，应思考圆心角为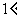的扇形面积圆

面积的几分之几？进而求出圆心角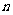的扇形面积.

如果设圆心角是n°的扇形面积为S，圆的半径为r，那么扇形的面积为

.

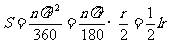因此扇形面积的计算公式为

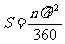　或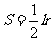

练习:1、如果扇形的圆心角是230°，那么这个扇形的面积等于这个扇形所在圆的面积的____________；

2、扇形的面积是它所在圆的面积的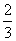，这个扇形的圆心角的度数是_________°.