1、用具体例子让学生体会反证法的思路

　　 思考：在△ABC中，已知AB＝c，BC＝a，CA＝b，且∠C≠90°.

　　 求证；a²+b²≠c².

　　 有些命题想从已知条件出发，经过推理，得出结论是很困难的，因此，人们想出了一种证明这种命题的方法，即反证法.

　　 假设a²+b²＝c²，则由勾股定理的逆定理可以得到∠C＝90°，这与已知条件∠C≠90°产生矛盾，因此，假设a²+b²＝c²是错误的.所以a²+b²≠c²是正确的.

2. 求证：在一个三角形中，至少有一个内角小于或等于60°

1.自学课本80页到81页，写下疑惑摘要：

P124~125　 8、9

(二)讲授新课

例6某工厂要加工一批密封罐，设计者给出了密封罐的三视图(如下图)，请你按照三视图确定制作每个密封罐所需钢板的面积.

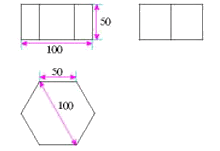
分析:对于某些立体图形，若沿其中一些线(例如棱柱的棱)剪开，可以把立体图形的表面展开成一个平面图形--展开图.在实际的生产中.三视图和展开图往往结合在一起使用.解决本题的思路是，由视图想象出密封罐的立体形状，再进一步画出展开图.从而计算面积.

　 解:由三视图可知，密封罐的形状是正六棱柱(如图(左)).

　　 密封罐的高为50mm，底面正六边形的直径为100mm.边长为50mm，图(右)是它的展开图.

由展开图可知，制作一个密封罐所需钢板的面积为

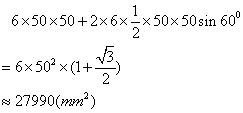
练习巩固

P122 练习

补充例题：根据下面三视图请说出建筑物是什么样子的?共有几层?一共需要多少个小正方体?

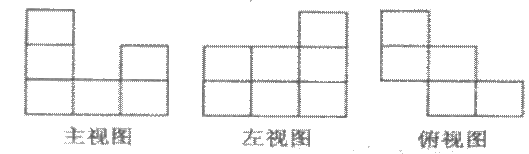
分析:由俯视图确定该建筑物在平面上的形状，由主视图、左视图确定空间的形状如图所示.

解:该建筑物的形状如图所示:

有3层，共9个小正方体.

思考：一个物体的主视图如上右图所示, 请画出它的俯视图，耐心想一想有

几种不同的情形?

(一)复习引入

1、完成下列练习

(1)、如图所示是一个立体图形的三视图，请根据视图说出立体图形的名称_______.

(2)、一张桌子摆放若干碟子，从三个方向上看，三种视图如下图所示，则这张桌子上共有________个碟子.

(3)、某几何体的三种视图分别如下图所示，那么这个几何体可能是( ).

(A)长方体 (B)圆柱 (C)圆锥 (D)球

2、让学生欣赏事先准备好的机械制图中三视图与对应立体图形的图片，借助图片信息让学生体会到本章知识的价值.并借此可以讲述一下现在一些中专、中技甚至大学里开设的模具和机械制图专业和课程就需要这方面的知识，激发学生的学习兴趣，导入本课.

重点：根据三视图描述基本几何体和实物原型及三视图在生产中的作用

难点：根据三视图想象基本几何体和实物原型的形状

3、了解将三视图转换成立体图开在生产中的作用，使学生体会到所学的知识有重要的实用价值.

2、经历探索简单的几何体的三视图的还原，进一步发展空间想象能力；

1、学会根据物体的三视图描述出几何体的基本形状或实物原型；