
1.(补充题)选择题:
(1)下列方程中,以1为解的方程是( )
A. 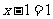 B.
B.  C.
C.  D.
D. 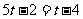
(2)下面有( )个方程的解为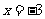 .
.
①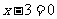 ;②
;②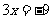 ;③
;③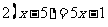 ;④
;④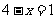
A. 1 B. 2 C. 3 D. 4
2.(补充题)检验下列各数是不是方程 的解:
的解:
(1)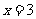 ;(2)
;(2)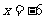 .
.
答案:1. B 2.(1)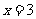 不是方程的解;(2)
不是方程的解;(2)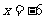 是方程的解.
是方程的解.
1. (补充题)选择题:
下列方程的解为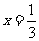 的是( ).
的是( ).
A. B.
B. C.
C.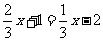 D.
D.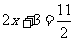
例1 教材P69 中 例1
分析:三个题目中的相等关系分别是:
(1)计算机已使用的时间+继续使用的时间=规定的检修时间.
(2)2(长+宽)=周长.
(3)女生人数-男生人数=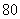 .
.
问题:列方程是解决问题的重要方法,利用所列的方程我们可以得出未知数的值,你能估算方程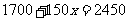 中的
中的 的值吗?
的值吗?
分析:方程中等号左边有未知数 ,估算的
,估算的 值代入方程应使等号左边
值代入方程应使等号左边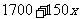 的值等于等号右边的值2450,这样的
的值等于等号右边的值2450,这样的 值才适合方程. 由于
值才适合方程. 由于 表示月份,是正整数,不妨让
表示月份,是正整数,不妨让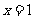 ,
,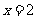 ,……分别代入方程算一算.
,……分别代入方程算一算.
由计算结果可以看到,每一个 的允许值都使代数式
的允许值都使代数式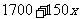 有一个确定的数值,为方便起见,可以列一个表格:
有一个确定的数值,为方便起见,可以列一个表格:
 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
… |
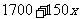 |
1850 |
2000 |
2150 |
2300 |
2450 |
2600 |
2750 |
… |
从表中发现:当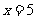 时,
时,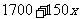 的值是
的值是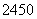 ,也就是,当
,也就是,当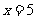 时,方程中等号的左边:
时,方程中等号的左边: 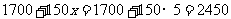 . 等号的右边:2450. 由此得到方程的左边=右边,就说
. 等号的右边:2450. 由此得到方程的左边=右边,就说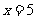 叫做方程
叫做方程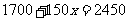 的解,也就是方程
的解,也就是方程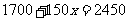 中,未知数
中,未知数 的值为5. 所以,方程的解就是
的值为5. 所以,方程的解就是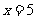 .
.
教材P71中的小云朵,可以多选几个情况来说明,以加强对方程解得意义的理解.
从表中你还能发现哪个方程的解?(引导学生得出)如方程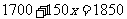 的解是
的解是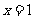 ;方程
;方程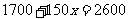 的解是
的解是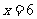 等等,使学生进一步体会方程解的概念.
等等,使学生进一步体会方程解的概念.
方程解的意义:使方程中等号左右两边相等的未知数的值,叫做方程的解.
教材P71的思考:你能估算方程 和方程
和方程 的解吗?通过估算这两个方程的解,你有什么想法?
的解吗?通过估算这两个方程的解,你有什么想法?
由于这两个方程估算其解有一定的困难,数不整齐,或方程比较复杂,出现矛盾冲突,引导学生得出:学习解方程的方法十分必要.
怎样检验一个数是否是方程的解呢?
例2(补充题) 检验下列各数是不是方程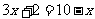 的解:
的解:
(1)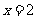 ;(2)
;(2)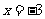 .
.
分析:要检验某一个数是不是方程的解,根据方程解的意义,应把这个数分别代入方程的左右两边,能使方程左右两边的值相等的未知数的值才是方程的解.
解:(1)把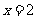 分别代入方程的左边和右边,得
分别代入方程的左边和右边,得
左边=3×2+2=8,右边=10-2=8.
∵ 左边=右边,
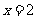 是方程
是方程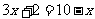 的解;
的解;
(2)把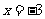 分别代入方程的左边和右边,得
分别代入方程的左边和右边,得
左边=3×(-3)+2=-7,右边=10-(-3)=13.
∵ 左边 右边,
右边,
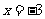 不是方程
不是方程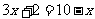 的解.
的解.
注意:强调检验的格式,分方程中等号的左边和右边,若把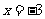 代入方程,不能左边和右边同时代入,写成
代入方程,不能左边和右边同时代入,写成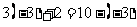 ,
,
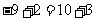 , 注意提醒学生在代入和计算中易出现的错误.
, 注意提醒学生在代入和计算中易出现的错误.
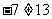 .
.
2.练习:当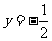 ,
,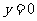 ,
,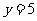 时,求式子
时,求式子 的值.
的值.
答案: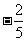 ,
,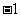 ,
,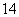 .
.
通过练习2强调求式子的值的一般步骤,其中易错易混的地方,如代入的值是负数,应加上括号,数与数相乘时应恢复乘号,运算关系不能混淆等.
复习:
1.什么是一元一次方程?
3.认知难点与突破方法
难点是方程解的意义和检验一个数是不是一个一元方程的解. 例1起着承上启下的作用,在估算方程解的过程中,理解方程解的意义,学会检验一个数是不是一个一元方程的解.抓住关键字“等号左右两边相等”,检验一个数是不是一个一元方程的解,要分别计算方程的左右两边,若其值相等,则这个未知数是方程的解,若不相等,则不是方程的解.
2.例、习题的意图
本节课重点是了解方程的解的意义. 通过实际问题中对所列方程解的估算,了解什么是方程的解以及由于估算遇到了困难,产生寻求方程解法的需求,为后面的学习做好铺垫.
例1是通过实际问题列出方程,根据(1)题未知数 的取值范围以及方程解的概念逐一代入方程来寻求方程的解,使学生亲身体验什么是方程的解,也为例2检验一个数值是不是方程的解做好铺垫. 对第(2)、(3)题再采用(1)题方法寻求方程的解已不容易,这又为后边学习解方程奠定了积极的心理储备.
的取值范围以及方程解的概念逐一代入方程来寻求方程的解,使学生亲身体验什么是方程的解,也为例2检验一个数值是不是方程的解做好铺垫. 对第(2)、(3)题再采用(1)题方法寻求方程的解已不容易,这又为后边学习解方程奠定了积极的心理储备.
例2是根据方程的解的意义,使学生会检验一个数值是不是方程的解,这一点应切实使学生掌握.
1.教学目标、重点、难点.
教学目标:
(1)了解方程的解的概念.
(2)体验对方程解的估算,会检验一个数是不是某个一元方程的解.
(3)渗透对应思想.
重点:方程解的意义,会检验一个数是不是一个一元方程的解.
难点:方程解的意义,会检验一个数是不是一个一元方程的解.
5. 教材P75习题2.1 5、6、7.
答案:1. 略. 2.
A 3. B
4. 设 天后两厂剩下原料相等,则有
天后两厂剩下原料相等,则有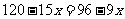 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com