例2　某面粉仓库存放的面粉运出　15%后，还剩余42　500千克，这个仓库原来有多少面粉？

　师生共同分析：

1．本题中给出的已知量和未知量各是什么？

在小学算术中，我们学习了用算术方法解决实际问题的有关知识，那么，一个实际问题能否应用一元一次方程来解决呢？若能解决，怎样解？用一元一次方程解应用题与用算术方法解应用题相比较，它有什么优越性呢？

为了回答上述这几个问题，我们来看下面这个例题．

例1　　　 某数的3倍减2等于某数与4的和，求某数．

(首先，用算术方法解，由学生回答，教师板书)

解法1：(4+2)÷(3-1)=3．

　答：某数为3．

　(其次，用代数方法来解，教师引导，学生口述完成)

解法2：设某数为x，则有3x-2=x+4．

解之，得x=3．

答：某数为3．

　纵观例1的这两种解法，很明显，算术方法不易思考，而应用设未知数，列出方程并通过解方程求得应用题的解的方法，有一种化难为易之感，这就是我们学习运用一元一次方程解应用题的目的之一．

　我们知道方程是一个含有未知数的等式，而等式表示了一个相等关系．因此对于任何一个应用题中提供的条件，应首先从中找出一个相等关系，然后再将这个相等关系表示成方程．

　本节课，我们就通过实例来说明怎样寻找一个相等的关系和把这个相等关系转化为方程的方法和步骤．

26、某地电话拨号上网有两种收费方式，用户可以任选其一：(A)计时制，0.05元∕分；(B)包月制，50元∕分(限一部个人住宅电话上网)；此外，每种上网方式都附加通信费0.02元∕分。

(1)某用户某月上网时间为x分钟，则该用户在A、B两种收费方式下应支付费用各多少元？

(2)如果一个月内上网200分钟和300分钟，按两种收费方式各需交费多少元？

(3)是否存在某一时间，会出现两种收费方式一样的情况吗？求出这时的上网时间？

(4)如果某人一个月上网20小时，那么应选用哪一种方式较为合算？如果小明的妈妈准备办理这种业务，你能告诉她如何选择更加合算吗？

《一元一次方程 3.1.1 3.1.2 等式的性质》测试卷答案

25.央行决定：从2007年12月21日起调整金融机构人民币存贷款基准利率，一年期存款基准利率由现行3.87%提高到4.14%，上调0.27个百分点；。所得利息要交纳5%的利息税。例如，存入一年期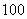元，到期储户纳税后得利息的计算公式为：

税后利息=100×4.14%×(1－5%)

已知某储户一笔一年期定期储蓄到期后交税后得利息393.3元.问该储户存了多少钱？

24.当x为何值时,式子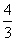x-5与3x+1的和等于9?

23.等式(k-2)x²+kx+1=0是关于x的一元一次方程(即x未知),求这个方程的解.

22.如果方程2x+k=x-1的解是x=-4,求3k-2的值.

21.利用等式的性质解下列方程.

　 (1)y+3=2；　　　　　　　　　　　　　　　　 (2)-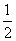y-2=3；　　　　　　

(3)9x=8x-6；　　　　　　　　　　　 　　　　　　(4)8m=4m+1。

18．小明说：“我发现一个结论：任何一个两位数，把它的十位上的数字与个位上的数字对调，得一个新的两位数，这个数与新两位数的和一定是11的倍数．”他的结论　 。(填正确或错误)

17.若x=2是关于x的方程2x+3k-1=0的解，则k的值是_______．