8.∵l²+m²=n²,∴l²=(n+m)(n-m).∵l为质数,且n+m＞n-m＞0,∴n+m=l²,n-m=1.于是l²=n+m=(m+1)+m=2m+1,2m=l²-1,2(l+m+1)=2l+2+2m=l²+2l+1=(l+1)².即2(l+m+1)是完全平方数.

7.简解:原方程变形为3x²-(3y+7)x+3y²-7y=0由关于x的二次方程有解的条件△≥0及y为整数可得0≤y≤5,即y=0,1,2,3,4,5.逐一代入原方程可知,原方程仅有两组解(4,5)、(5,4).

6.8888≡8(mod37),∴8888²²²²≡8²(mod37).

7777≡7(mod37),7777³³³³≡7³(mod37),8888²²²²+7777³³³³≡(8²+7³)(mod37),而8²+7³=407,37|407,∴37|N.

5.先求出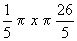,然后将方程变形为y=5+x-2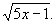要使y为整数,5x-1应是完全平方数,…,解得

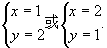
4.可仿例2解.

3.不妨设x≤y≤z,则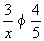,故x≤3.又有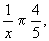故x≥2.若x=2,则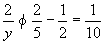,故y≤6.又有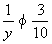,故y≥4.若y=4,则z=20.若y=5,则z=10.若y=6,则z无整数解.若x=3,类似可以确定3≤y≤4,y=3或4,z都不能是整数.

2.(1)9及1.　　 (2)9.　　 (3)4.

(4)原方程可变形为x²=(7y+1)²+2y(y-7),令y=7可得x=50.

1.D.C.

9.(1988年全国初中数学竞赛题)如果p、q、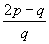、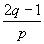都是整数，并且p＞1，q＞1，试求p+q的值.

练习二十

8．(1985年上海初中数学竞赛题)已知直角三角形的两直角边长分别为l厘米、m厘米，斜边长为n厘米，且l，m，n均为正整数，l为质数.证明：2(l+m+n)是完全平方数.