1．实验演示

　 教师先提出实验的要求：请同学们仔细观察实验的过程，思考能否从中发现规律，再用自己的语言叙述你发现的规律．然后按如图的方法演示实验．

　 ( 教师可以进行两次不同物体的实验，学生独立思考，小组交流，代表发言．)

用估算的方法我们可以求出简单的一元一次方程的解．你能用这种方法求出方程0.28-0.13y=0.27y+1的解吗？

　第(1)题要求学生给出解答，第(2)题较复杂，估算比较困难，此时教师提出：我们必须学习解一元一次方程的其他方法．

6、缩减了小组合作学习研讨的时间，没能体现小组合作的优势。

2008-11-14

4、对于性质1中的“式子”未能做到合理的解释。 　　 5、对于性质的运用，我采用老师问学生答的形式，缺少学生板演的环节，没有照顾到全体学生的参与。

1、不能正确的把握操作的时间，导致延迟了大概5分钟下课。作为教师所演示的实验操作的难易程度，应和所给的讨论时间成正比。这样既保证了实验的有效性，又不至于浪费时间。在探索等式性质中用天平演示实验之后留给学生思考和讨论的时间并不是十分充足，使活动没有真正起到最初的效果。而其后在训练的时候留给学生思考和解决问题的时间也略显不足。 　　 2、教学中没能注重学生思维多样性的培养。数学教学的探究过程中，对于问题的最终结果应是一个从“求异”逐步走向“求同”的过程，而不是在一开始就让学生沿着教师预先设定好方向去思考，这样控制了学生思维的发展。如在研究等式性质1的过程，我是步步指导，层层点拔，惟恐有所纰漏，使得学生的思维受到了限制。 　　 3、在课堂上对突发的事件处理不够果断，对学生的回答没有及时反馈。如在练习2中要求学生同时根据等式的两个性质编一个新的等式时，学生的解答出现了多种结果，老师的点评和引导所花的时间过多(约5分钟)，打乱了下一步的安排。

4．若a＞0，b＜0，则方程｜x-a｜+｜x-b｜=a-b的解是什么？

3．解下列不等式：

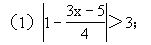
　(2)5≤｜5x-3｜≤10；

　(3)｜x+1｜+｜4-x｜＜6；

　(4)｜｜x-1｜-｜x+2｜｜＞1．

2．解方程组：

1．解下列方程：

　(1)｜x+3｜-｜x-1｜=x+1；

　(2)｜｜1+x｜-1｜=3x；

　(3)｜3x-2｜-｜x+1｜=x+2；

　(4)｜3y-2｜=-｜5x-3｜．

9.易知p≠q,不妨设p＞q.令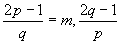=n,则m＞n由此可得不定方程(4-mn)p=m+2,解此方程可得p、q之值.