
1.填空题
(1)将等式x-3=5 的两边都__________得到x=8 ,这是根据等式性质______.
(2)将等式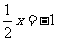 的两边都乘以____________、或除以___________得到x=-2,这是根据等式性质____________;
的两边都乘以____________、或除以___________得到x=-2,这是根据等式性质____________;
(3)将等式x+y=0的两边都____________得到x=-y,这是根据等式性质_____________;
(4)将等式xy=1的两边都__________得到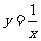 ,这是根据等式性质________.
,这是根据等式性质________.
4.运用前面所学过的内容解方程
2x2-3x-1+4x-3x2=-x2-(x+1)
3.判断下列变形是否正确
(1)由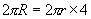 得到
得到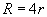 .( )
.( )
(2)由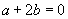 得到
得到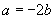 .( )
.( )
(3)由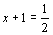 得到
得到 .( )
.( )
(4)由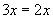 得到
得到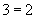 .( )
.( )
(5)由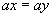 得到
得到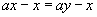 .( )
.( )
2.用适当的整式填空,使所得结果仍是等式
(1)如果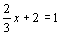 ,那么
,那么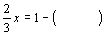 ;
;
(2)如果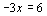 ,那么
,那么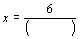 ;
(3)如果
;
(3)如果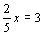 ,那么
,那么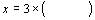 ;
;
(4)如果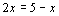 ,那么
,那么 ;
(5)如果
;
(5)如果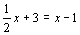 ,那么
,那么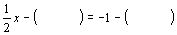 .
.
1.填空题
(1)将等式x-3=5 的两边都__________得到x=8 ,这是根据等式性质______.
(2)将等式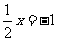 的两边都乘以____________、或除以___________得到x=-2,这是根据等式性质____________;
的两边都乘以____________、或除以___________得到x=-2,这是根据等式性质____________;
(3)将等式x+y=0的两边都____________得到x=-y,这是根据等式性质_____________;
(4)将等式xy=1的两边都__________得到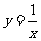 ,这是根据等式性质________.
,这是根据等式性质________.
|
问题与情景 |
师生行为 |
设计意图 |
|
(-)创设情境,复习导入 教师在上课开始时,给出如下的数学关系 (出示投影) 1+2=3; 3x=5 ; a+b=b+a ;6=2×3 ; S=ab ; 4+x=7 演示实验: 天平两边各放2个砝码,现在我们再分别拿出1个砝码,放入天平两边,问天平两边重量的关系?如果我们将两边的砝码各拿走1个又会怎样呢? 天平两边重量扩大到原来的3倍,或缩小到原来的3倍,结果又会怎样呢?  (二)探索新知,讲授新课 提出问题:由上面两组等式变形,我们可以得出关于等式变形什么结论?把上面式中的1,改3或-5行吗? 提出问题: ①4=4两边都加上整式如:两边都加上2a 结果还是等式吗? ②第二结论中所说除数可以是零吗? (三)尝试反馈,巩固练习 (出示投影) 1.判断:已知等式a=b ,下列等式是否成立? ①a+2=b; ②a+2=b-2; ③a+2=b+3;④-2a=-2b 2.若a=b ,请同学们分别根据等式的两个性质编出两个新的等式并说出你的编写根据. (出示投影) 1.从x=y 能不能得到x+5=y+5 呢?为什么? 2.从x=y 能不能得到 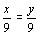 呢?为什么? 呢?为什么?3.从a+2=b+2 能不能得到a=b 呢?为什么? 4.从-3a=-3b 能不能得到a=b 呢?为什么? 5.由ax=ay,能不能得到x=y呢?为什么? (出示投影) 例1 用适当的数或整式填空,使所得结果仍是等式 1.若3x+5=9,那么3x=9- ; 2.若2x=5-3x,那么2x+ =5 ; 3.如果0.2x=10 ,那么x= . 巩固练习:(出示投影) 练习:用适当数填空,并且说出根据等式的哪条性质及怎样变形的? 1.如果2x+7=10,那么2x=10- ; 2.如果5x=4x+7,那么5x- =7; 3.如果-3x=18,那么x= ; 4.如果a+8=b,那么a= ; 5.如果 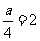 ,那么a= . ,那么a= .(四)变式训练,培养能力 (出示投影) 例2 利用等式的性质解方程: (1) 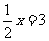 ; ; (2) 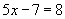 ; ;(3)4x=5x+7 (出示投影) 1.利用等式的性质解下列方程 (1) x-5=6 (2)0.3x=45 (3)-y=0.6 (4) 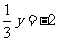 2.应用本节知识解方程: 3-4x=4-6x (五)归纳小结 (出示投影) |
师提出问题:观察上面式子表示了什么关系?由学生回答“相等关系”后引出等式的概念和等式的含义,分清等式的左边和右边. 教师和学生一起完成 教师引导学生,把上面实验抽象为一个数学问题. 即:2=2. 学生活动:让全体学生参与讨论,启发学生怎样用精炼的语言叙述,或分组推荐代表回答. 师总结等式的性质: 由前两式总结:1.等式的两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式. 由后两式总结:2.等式的两边都乘以(或除以)同一个数(除数不能为零),所得结果仍是等式. 学生活动:学生回答问题后,教师对上面结论加以补充说明. 教师归纳:以上两个规律,就是我们今天学习的“等式性质” 学生活动:分组抢答. 注意引导学生归纳出等式性质得“三同”,即等式两边同时进行同一种运算,加(或减)、乘以(或除以)的是同一个数. 注意学生在回答中出现的问题,及时反馈。 教师总结:从以上题目可知,根据等式的性质,从已知等式出发通过变形可得出新的等式. 教师帮助学生分析,并提出问题引导学生回答: 1题从已知的一边入手3x+5 怎样变形就得到3x 呢?(原等式两边都减去5)根据___________? 2题观察等式的右边怎样由5-3x 变形成5(两边加上3x ),即原来两边都加上3x ,根据等式性质1. 3题观察等式左边怎样由0.2x 变形为x ,即等式两边都除以0.2,根据等式性质2. 学生活动:分组讨论回答 教师指导解答,最后应用由学生代表性地评比一下,以培养学生灵活性、多角度思考数学问题的方法. 我们通过学习等式的性质,不难发现可以利用等式的性质解决方程的求解问题(也就是可以求方程未知数的值). (1) ; 解:等式两边都乘以 2 得x = 6 (2)5x-7=8 ; 解:等式两边都加上 7 得 5x=8+7 等式的两边都除以5 得x=3 . (3) 4x=5x+7 解:等式两边同时减去5x 得 4x-5x=7 化简得 –x=7 等式两边同时乘以(-1) 得 x=-7 邀请学生板演,注意规范格式。 教师小结:我们今天学习了等式的概念和等式的性质,通过学习我们应该清楚: 1.能根据等式的性质,把已知等式通过变形得到一个新等式,问题的关键在于怎样从新等式出发考虑用什么性质变形,这要靠大家的观察分析能力. 2.我们今天学习的等式的性质,是将来解方程的依据. |
复习等式概念。 通过演示实验得到结论。有效地引导学生观察、类比,从而发现规律,鼓励学生用自己的语言表达。 通过以上两条性质的总结,教师应强调以下四点: ①等式的性质1是加法和减法运算,等式的性质2是乘法或除法运算. ②等式的两边都参与运算,并且是同一种运算. ③加(或减)、乘以(或除以)的是同一个数. ④零不能做除数或分母. 由于这组题是例题的巩固,因此可以由学生讨论分组,以竞赛形式回答以增加课堂上的参与意识. 这组题是对等式性质的辨析,教学时应多让学生思考,并能说出依据. 注意第5小题学生可能会产生错误,老师应注意强调除数不能为零。 例一中得第3小题还可以在等式两边分别乘以5.注意引导学生区分什么时候用乘法,什么时候用除法可以简化运算。 这一段是学生尝试利用等式性质对等式变形的练习过程,因此可采用小组竞赛、抢答等灵活的课堂训练形式. 1.题目可启发学生思考如何应用等式性质求方程中未知数的值,由学生思考后教师引导作答写出过程 2.点出解方程得目标是通过变形得到形如x=a得结果。 3.注意提醒学生解方程后应进行检验。 练习1是利用等式变形来解方程,注意和小学的解法加以区分。 练习2涉及到两次变形以及合并同类项,注意引导学生理解. |
师生共同做演示实验,得出等式性质,教师出示巩固性练习,学生以多种形式完成.
投影仪或电脑、简单实物.
=c的形式。并且a,b,c,x都是非负数,解方程则是利用加法与减法互为逆运算,乘法与除法互为逆运算来进行的。本课的主要内容是等式和它的性质。 2.等式的定义是通过列举各种等式的具体例子,用描述性语言给出的。学生能认识到等式的意义,并能举出例子就可以了。不必过多地引伸,如不必把等式分为绝对等式,条件等式和矛盾等式。 3.等式的性质是利用天平实验引入的。由于不讲方程的同解原理,等式的性质就成为解方程的根据。因此,等式性质1指出等式两边不仅都可以加上(或减去)同一个数,而且还可以都加上(或减去)同一个式子,但等式性质2则只说等式两边可以乘(或除以)同一个数(除数不能是0)。根据等式的性质,可以从一个已知的等式出发,得出新的等式,对一个方程进行有目的的适当变形,就可以求出它的解来。
3.疑点:(1)等式性质2中,关于除数不为零的理解.
(2)利用性质变形时,对“等式两边”的理解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com