
4、(6分)如果连接梯形两腰的中点,把这条线段叫做梯形的中位线,那么梯形的中位线有什么特征呢?
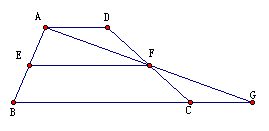
如图,梯形ABCD中,AD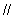 BC、点E、F分别为两腰AB、CD的中点。
BC、点E、F分别为两腰AB、CD的中点。
猜想:EF= 。
下面我们按如下思路探究
(1)
连接AF并延长交BC的延长线于G,你发现 ADF和
ADF和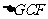 有怎样的关系?证明你的结论。(2)由①的结论,可以得出EF是
有怎样的关系?证明你的结论。(2)由①的结论,可以得出EF是 ABG中的怎样的线段?(3)由此你能证明你的猜想吗?试把猜想证明完毕。
ABG中的怎样的线段?(3)由此你能证明你的猜想吗?试把猜想证明完毕。
3、(6分)已知:如图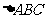 的三边长分别为a、b、c,它的三条中位线组成一个新的三角形,这个新三角形的三条中位线又组成了一个小三角形。(1)求这个小三角形的周长。(2)照上述方法继续做下去,到第
的三边长分别为a、b、c,它的三条中位线组成一个新的三角形,这个新三角形的三条中位线又组成了一个小三角形。(1)求这个小三角形的周长。(2)照上述方法继续做下去,到第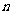 次时,这个小三角形的周长是多少?
次时,这个小三角形的周长是多少?
2、(3分)已知:如图,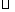 ABCD的边AB在
ABCD的边AB在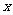 轴上,顶点D在
轴上,顶点D在 轴上,AD=4,AB=5,点A的坐标为(-2,0),求:点B、点C、点D的坐标。
轴上,AD=4,AB=5,点A的坐标为(-2,0),求:点B、点C、点D的坐标。

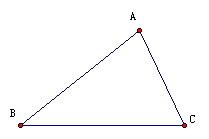
1、(3分)如图是一块三角形的菜地,请你将这块菜地平均分成面积相等的四部分。(至少要用两种不同的方法)
1.如图3-8,平行四边形ABCD中,E、F分别是AB、CD上的点,且BE = CF,
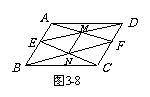 AF、DE相交于M,BF、CE相交于N. 求证:MN .
AF、DE相交于M,BF、CE相交于N. 求证:MN .
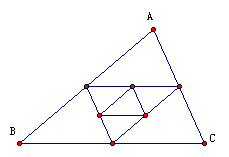
2.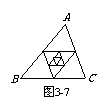 如图3-7,△ABC的三边长为a、b、c,它的三条中位线组成一个新的三角形,新三角形的三条中位线又组成一个三角形,……
以此类推,第五次组成的三角形的周长是( ).
如图3-7,△ABC的三边长为a、b、c,它的三条中位线组成一个新的三角形,新三角形的三条中位线又组成一个三角形,……
以此类推,第五次组成的三角形的周长是( ).
A. 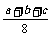 B.
B.
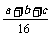
C.  D.
D.
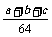
1.已知:△ABC的周长等于16,D、E分别是AB、AC的中点,那么,△ADE的周长等于( );
A. 4 B. 6 C. 8 D. 10
2.△ABC三条中位线构成的三角形的周长为18,则△ABC的周长是 .
1.顺次连接四边形各边中点所得到的四边形是 四边形;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com