
(五)布置作业
(四)小结
本节课我们学习了如下内容.
1.练习了解一元一次不等式组.
2.总结了由两个一元一次不等式所组成的不等式组的解集的四种情况.
(三)学生练习
(1)解下列不等式组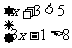
(2)求不等式 的整数解。
的整数解。
(二)尝试探索,讨论解的情况
[师]我们从每个不等式的解集,到这个不等式组的解集,认真观察,互相交流,找出规律.
(1)由 得x>1;
得x>1;
(2)由 ;
;
(3)由 得
得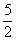 <
< ;
;
(4)由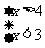 得,无解.
得,无解.
[生]由(1)得,两个不等式的解集中不等号的方向都是大于号,在数字1和-4中取大数1,不等号取大于号.
由(2)得,两个不等式的解集中不等号的方向都是小于号,在不等式组的解集中不等号的方向取小于,而取较小的数字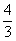 .
.
由(3)得,两个不等式的解集中不等号的方向有大于也有小于,数字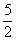 <4,并且是x>
<4,并且是x>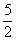 ,x≤4,最后的结果中是x取大于小数小于大数,即
,x≤4,最后的结果中是x取大于小数小于大数,即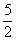 <x≤4.
<x≤4.
由(4)得,两个不等式的解集中不等号的方向有大于也有小于,并且是x>4,x<3,因为4>3,即x应取大于4而小于3的数,而这样的数根本不存在,所以原不等式组的解集为无解.
[师]大家分析得非常精彩.基本上说明了情况,下面我系统地给大家作一总结:
两个一元一次不等式所组成的不等式的解集有以下四种情形:( )
)
(1)
不等式组 的解集是
的解集是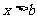 ;
;
(2)
不等式组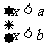 的解集是
的解集是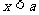 ;
;
(3)
不等式组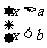 的解集是
的解集是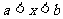 ;
;
(4)
不等式组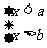 的解集是无解。
的解集是无解。
[师]这是用式子表示,也可以用语言简单表述为:
大大取大;小小取小;
大小小大取中间;
大大小小数无解.
[师]求上第三题的整数解。
(一)创设问题情境,导入新课
[师]上节课我们已经学习了由两个一元一次不等式组成的不等式组的解法,本节课我们将继续加强解法的熟练性和准确性,同时还要全面地对所有解的情况进行总结.
(板书)解下列不等式组(1)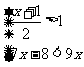 (2)
(2) (3)
(3) (4)
(4)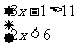
[师]在做这组练习题之前,我们先回忆一下求一元一次不等式的解集和一元一次不等式组的解集的步骤.
[生]解一元一次不等式的步骤为:去分母,去括号,移项、合并同类项,系数化成1.要注意的是在去分母和系数化成1这两步中不等号方向是否改变.
解一元一次不等式组的步骤为:分别求出两个一元一次不等式的解集,在数轴上确定它们的公共部分,从而得出不等式组的解集.
[师]好.下面我们先自己独立完成这四个不等式组的求解.
(三)情感态度与价值观:1.加强运算的熟练性与准确性.
2.培养思维的全面性.
(二)过程与方法:通过总结解一元一次不等式组的步骤,培养学生全面系统的总结概括能力.
(一)知识与技能: 1.进一步巩固解一元一次不等式组的过程.
2.总结解一元一次不等式组的步骤及情形.
4.拓展练习,培养能力
①已知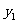 =3(5-2x),
=3(5-2x), 2(5x+
2(5x+ ),当x为何值时,满足
),当x为何值时,满足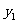 <
< 。
。
②已知关于x的方程  的解是非负数,求a的取值范围
的解是非负数,求a的取值范围
[教法说明]
3.例题讲解,巩固知识
解下列不等式,并把它们的解集在数轴上表示出来.
① ;
②
;
②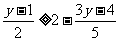 ;
;
[教法说明]教学时,应强调去分母的依据,在解第二题时强调不含分母的项也要乘以公分母,另还要注意在必要时候要添括号!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com