2 一元一次方程的讨论——青夏教育精英家教网—

2.2　一元一次方程的讨论(1)(一)

5.作业

见作业本。

4.课堂小结：

小结的要点如下：这一课主要学习如何列代数式，其关键在于仔细审题，弄清题意；正确找出题中的数量关系和运算顺序，为避免弄错运算顺序，对于一些容易混淆的说法，要仔细进行对比。

1. (1)代数式6p可以表示什么?

　　 (2)一个两位数的个位数字是a,十位数字是b，请用代数式表示这个两位数;

　　(3)如何用代数式表示一个三位数?

　 (4)代数式(1+8%)x可以表示什么?

　 (5)用具体数值代替(1+8%)x中的x,并解释所得代数式值的意义.

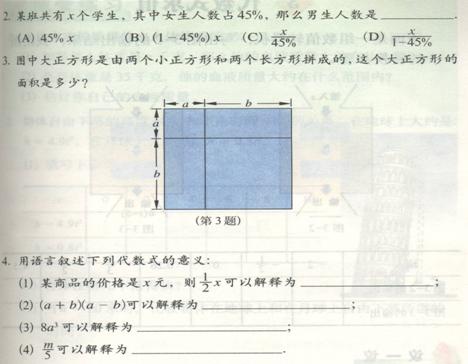
3. 随堂练习:

1.　　　讲解例题：

例1　列代数式,并求值.

(1)某公园的门票价格是:成人票每张10元,学生票每张5元.一个旅游团有成人x人,学生y人,那么该旅游团应付多少门票费？

(2)如果该旅游团由37个成人、15个学生，那么他们应付多少门票费？

解：(1)该旅游团应付的门票费是(10x+5y)元。

2)把x=37，y=15代入代数式10x+5y，得

　　10×37+5×15=445。

　因此，他们应付445元门票费。

想一想：代数式还可以表示什么？你能举出其它的例子吗?

解：(1)用c表示蟋蟀1分叫的次数，则该地当时的温度为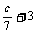

解：(1)1.2÷ 2= 　,即此时张宇的身高是他影长的倍.

　　　　　 (2)此时此地物体的高度为 l米.

(3)将l=5.5代入　 l,得×5.5=3.3(米)

因此,建筑物此时的高度是3.3米.

1. 代数式(algebraic expression)：像2(m+n), 4+3(x-1),x+x+(x+1), a³ ,a+b,ab, 等式子都是代数式.

单独一个数或一个字母也是代数式.如2.6,a,-7,0等.

注意:a× b通常写作ab;1÷a通常写作 ;数字通常写在字母的前面.

首先提出问题，说明为什么要学习代数式。强调在解决一些实际问题时，往往需要先把问题中与数量有关的词语，用含有数、字母和运算符号的式子表示出来，也就是列出代数式。

注意：上述说法，既是本课的引人，又是代数式概念的深化，因为它已具体涉及代数式的特点：含有数、字母和运算符号，从而为在本章的“小结与复习”里提出代数式的定义作了铺垫。

教　　　学　　　后　　　记
　

3.2代数式

题目	3.2代数式
教学目标	了解代数式、单项式、单项式的系数、多项式、整式的概念能用单项式表示简单问题的数量关系能解释一些简单代数式的实际背景或几何意义通过具体例子感受“同一个代数式可以表示不同的实际意义”，“理解符号所代表的数量关系”
教学重点	用单项式表示简单问题的数量关系
教学难点	解释一些简单代数式的实际背景或几何意义
教学方法	引导发现式
教学工具
教学内容	教师活动	学生活动