3、会用移项法则解方程

数学思考：1、学习分析问题找到相等关系并通过方程解决问题的方法

2、理解移项法，并知道移项法的依据

2.2.2　 从古老的代数书说起-- 一元一次方程的讨论(1)(第2课时)

知识技能：1、经历运用方程解决问题的过程，发展抽象、概括，分析问题和解决问题的能力，认识用方程解决实际问题的关键是建立相等关系

0.6t=50+0.4t

　 移项得 0.6t－0.4t=50

　 合并，得0.2t=50

　 系数化为1，得t=250

答：如果一个月内通话250分，那么两种计费方式的收费相同。

4、　 对于某个本地通通话时间，会出现两种计费方式的收费一样的情况吗？

4，　 设累计通话t分，则用“全球通”要收费(50+0.4t)元，用“神州行”要收费0.6t元，如果两种计费方式的收费一样，则

3、　 一个月内在本地通话200分和300分，按两种计费方式各需交费多少元？

2、　 猜一猜，使用哪一种计费方式合算？

1、　 你能从中表中获得哪些信息，试用自己的话说说。

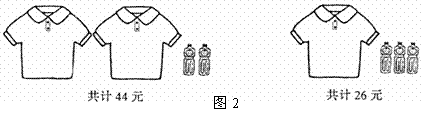
26，根据如图2给出的信息，求每件T恤衫和每瓶矿泉水的价格.

27，用8块相同的长方形地砖拼成一块矩形地面，地砖的拼放方式及相关数据如图3所示，求每块地砖的长与宽.

28，初三(2)班的一个综合实践活动小组去A，B两个超市调查去年和今年“五一节”期间的销售情况，如图4是调查后小敏与其它两位同学进行交流的情景。根据他们的对话，请你分别求出A、B两个超市今年“五一节”期间的销售额.

29，某纸品加工厂为了制作甲、乙两种无盖的长方体小盒(图5), 利用边角料裁成正方形和长方形两种硬纸片,长方形的宽和正方形边长相等(图6),现将150张正方形纸片和300张长方形纸片全部用于制作这种小盒,求可做成甲、乙两种小盒各多少个?

30，甲、乙两同学从A地到B地,甲步行速度为每小时3千米,乙步行的速度为每小时5千米,两人骑自行车的速度都是每小时15千米,甲先步行,乙先骑自行车, 两人同时出发,走了一段路程后,乙下车步行,甲走到乙放车处骑自行车,以后不断交替行进,两人最后恰好同时到达B地,求甲走完全程的平均速度.

31，某电视台在黄金时段的2分钟广告时间内，计划插播长度为15秒和30秒的两种广告.15秒广告每播1次收费0.6万元，30秒广告每播1次收费1万元.若要求每种广告播放不少于2次.问：

(1)两广告的播放的次数有几种安排方式？

(2)电视台选择哪种方式播放收益较大？

32，“利海”通讯器材商场，计划用60 000元从厂家购进若干部新型手机，出厂价分别为甲种型号手机每部1 800元，乙种型号手机每部600元 ，丙种型号手机每部1200元.若商场同时购进其中两种不同型号的手机共40部，并将60 000元恰好用完，请你帮助商场计算一下如何购买.

33，有甲、乙、丙三种规格的钢条，已知甲种2根，乙种1根，丙种3根，共23米；甲种1根，乙种4根，丙种5根，共36米.问甲种1根，乙种2根，丙种3根，共多少米？

34，甲、乙两班学生到集市上购买苹果,苹果价格如下:

甲班分两次共购买苹果70kg(第二次多于第一次),共付出189元, 而乙班则一次购买苹果70kg问:

　　 (1)乙班比甲班少付出多少元?