
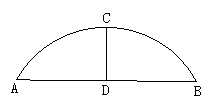
6.已知:如图2,有一圆弧形拱桥,拱的跨度AB=16cm,拱高CD=4cm,那么拱形的半径是____m.
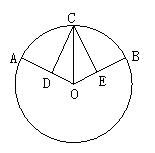
5.如图1,⊙O的直径为10,弦AB=8,P是弦AB上的一个动点,那么OP长的取值范围是_____.

(1) (2) (3)
4.已知⊙O中,OC⊥弦AB于C,AB=8,OC=3,则⊙O的半径长等于________.
3. 圆的一条弦把圆分为5: 1 两部分, 如果圆的半径是2cm, 则这条弦的长是_____cm.
2.已知⊙O的半径为R,弦AB的长也是R,则∠AOB的度数是_________.
1.圆既是轴对称图形,又是_________对称图形,它的对称轴是_______, 对称中心是____.毛
1.2二次根式的乘除法
|
教学内容 |
1.2二次根式的乘除法 |
课型 |
新授课 |
主备人 执教人 |
|
|
教学目标 |
理解二次根式乘法、除法运算的一般规律,会应用两个公式进行二次根式的乘除法运算。 |
||||
|
过程与方法 |
通过试一试,比较、归纳等活动,经历、感受并总结出二次根式的乘法和除法运算公式,运用这两个公式对二次根式进行化简。 |
||||
|
教具准备 |
多媒体,学案. |
||||
|
教学过程 |
师生活动 |
||||
|
一、复习旧知 |
1.什么是二次根式? 2.二次根式有哪些性质? 2.二次根式有哪些性质?(1) (2) (3) |
||||
|
二、探索新知 |
1、二次根式的乘法公式: 2、例1 计算: (1) 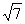 × ×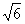 ; (2) ; (2)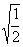 × × 3、练习: (1)  (2) (2)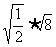 (3) (3)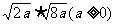 4、二次根式性质4: 
利用它可以进行二次根式的化简.例如:  =
= |
||||
|
5、例2:化简. (1) 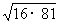 (3)
(3) 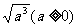  (2) (2) 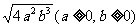 6、例3:化简.  |
|||||
|
|
6、练习. 1.化简: (1) 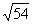 (2)
(2)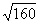 (3) 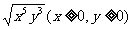 (4) (4) 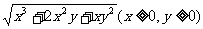 2.计算: (1)  (2)
(2)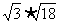 (3)
(3)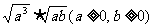 |
||||
|
7、二次根式的除法法则: 8、例3:计算 (1)  (2)
(2)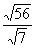 (3)  (4)
(4)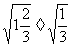 9、二次根式性质5: 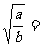 (
)
(
)利用它可以进行二次根式的化简. 10、化简: (1) 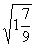 (2)
(2)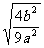 11、分母有理化: (1) 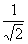 (2) (2) (3) (3) |
|||||
|
三、课后作业 (满分:100分) |
1 化简: (1) 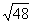 (2)
(2)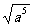 (3) (3)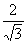 . .(4)  (5)
(5)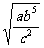 2. 计算: (1) 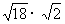 (2) (2)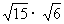 (3) (3)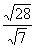 ; ;(4) 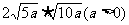 (5) (5) 3.(探究题)如图1-2-4所示,在△ABC中,∠B=90○ ,点P从点B开始沿BA边向点A以1厘米/秒的宽度移动;同时,点Q也从点B开始沿 BC边向点C以 2厘米/秒的速度移动,问几秒后,△PBQ的面积为36平方厘米? 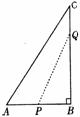 |
教后感:
二次根式除法运算如何进行?对于简单的二次根式如何逆用二次根式除法运算法则进行化简?
2.小明在学习了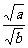 =
=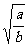 (a≥0,b>0)后,认为
(a≥0,b>0)后,认为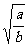 =
=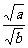 也成立,因此他认为:
也成立,因此他认为: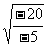 =
=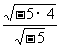 =
=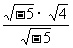 =
=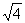 =2是正确的,你认为他的化简对吗?说说你的理由。
=2是正确的,你认为他的化简对吗?说说你的理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com