
1.进一步体会证明的必要性以及计算与证明在解决问题中的作用.
2.特殊平行四边形(一)
矩形
知识与技能目标:
经历探索、猜想、证明的过程,进一步发展推理论证能力。
过程与方法目标:
能够用综合法证明矩形性质定理和判定定理.
情感态度与价值观目标:
3.2 特殊平行四边形(一)
|
课 题 |
3.2 特殊平行四边形(一) |
课型 |
新授课 |
|
|
教学目标 |
1.经历探索、猜想、证明的过程,进一步发展推理论证的能力。 2.能运用综合法证明矩形性质定理和判定定理。 3.体会证明过程中所运用的归纳概括以及转化等数学思想方法。 |
|||
|
教学重点 |
掌握矩形的性质和判定以及证明方法。 |
|||
|
教学难点 |
运用综合法证明矩形性质和判定。 |
|||
|
教学方法 |
讲练结合法 |
|||
|
教学后记 |
|
|||
|
教 学 内 容 及 过 程 |
备注 |
|||
|
一、回顾交流 1.你了解哪些特殊的平行四边形? 2.这些特殊的平行四边形与平行四边形有哪些关系? 3.能用一张图来表示它们之间的关系吗? 学生回忆,回答。 平行四边形与矩形、菱形、正方形的关系。 二、小组活动 提问:矩形有哪些性质? 学生回忆,回答。 定理 矩形的四个角都是直角。 定理 矩形的对角线相等。 学生先独立证明上述两个定理,再进行交流。 议一议    如图,设矩形的对角线AC与BD的交点为E, 如图,设矩形的对角线AC与BD的交点为E,那么BE是Rt△ABC中一条怎样的特殊线段? 它与AC有什么大小关系?为什么? 学生分四人小组进行合作交流,相互补充。 推论:直角三角形斜边上的中线等于斜边的一半。 三、范例学习    例1,如图,矩形ABCD的两条对角线相交于点O,已知∠AOD=120°,AB=2.5cm,求矩形对角线的长。 例1,如图,矩形ABCD的两条对角线相交于点O,已知∠AOD=120°,AB=2.5cm,求矩形对角线的长。拓展:例1还可以怎么证?与同伴交流。 四、随堂练习 课本随堂练习 1、2 五、课堂总结 矩形具有平行四边形的所有性质,还具有自己独有的性质:四个角都是直角,对角线相等。 六、布置作业 课本习题3.4 1、2、3 |
|
|||
 已知:如图3-19,△ABC中,∠BAC
= 90°,分别以AB、BC为边作正方形
已知:如图3-19,△ABC中,∠BAC
= 90°,分别以AB、BC为边作正方形
|
纠正错解 |
|
|
|
点 评 |
|
|
ABDE和正方形BCFG,延长DC、GA交于点P. 求证:PD⊥PG.
[综合练习]
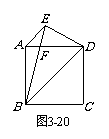 已知:如图3-20,正方形ABCD中,AE∥BD,BE = BD,BE交AD于F. 求证:DE = DF.
已知:如图3-20,正方形ABCD中,AE∥BD,BE = BD,BE交AD于F. 求证:DE = DF.
[探究练习]
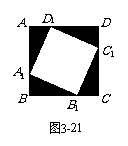 如图3-21,要把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1,试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原正方形面积的,请说明理由.
如图3-21,要把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1,试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原正方形面积的,请说明理由.
练习三
[基础练习]一、1. 112.5; 2. 正方形,正方形; 3. 2a. 二、1. A; 2. D. 三、提示:证△ABG ≌△DBC.
[综合练习]提示:先证∠DBE = 30°.
[探究练习]提示:AA1 = BB1 = CC1 = DD1 = (或= ).
2.四边形ABCD的对角线AC = BD,且AC⊥BD,分别过A、B、C、D作对角线的平行线,则所构成的四边形是( ).
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
1.四边形ABCD中,AC、BD相交于O,下列条件中,能判定这个四边形是正方形的是( );
A. AO = BO = CO = DO,AC⊥BD B. AB∥CD,AC = BD
C. AD∥BC,∠A =∠C D. AO = CO,BO = CO,AB = BC
3.正方形边长为a,若以此正方形的对角线为一边作正方形,则所作正方形的对角线长为 .
2.已知: ABCD中,对角线AC、BD相交于O. ①若OA = OB,且OA⊥OB,则四边形ABCD是 ,②若AB = BC,且AC = BD,则四边形ABCD是 ;
1. 在正方形ABCD的AB边的延长线上取一点E,使BE = BD,连接DE交BC于F. 则∠BFD = °;
在正方形ABCD的AB边的延长线上取一点E,使BE = BD,连接DE交BC于F. 则∠BFD = °;
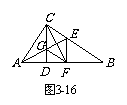 如图3-16,CD是Rt△ABC的斜边AB上的高,∠A的平分线AE交CD于G,∠BCD的平分线交BD于F,求证:四边形CEFG是菱形.
如图3-16,CD是Rt△ABC的斜边AB上的高,∠A的平分线AE交CD于G,∠BCD的平分线交BD于F,求证:四边形CEFG是菱形.
|
纠正错解 |
|
|
|
点 评 |
|
|
[综合练习]
 如图3-17,将矩形ABCD折叠,使顶点B与D重合,折痕为EF,连接BE、DF.
如图3-17,将矩形ABCD折叠,使顶点B与D重合,折痕为EF,连接BE、DF.
(1)四边形BEDF是什么四边形?为什么?
(2)若AB = 6cm,BC = 8cm,求折痕EF的长.
[探究练习]
 已知:如图3-18,D是等腰Rt△ABC的直角边BC上一点,AD的垂直平分线EF分别交AB、AC于点E、F,BC = 2,CD = a.
已知:如图3-18,D是等腰Rt△ABC的直角边BC上一点,AD的垂直平分线EF分别交AB、AC于点E、F,BC = 2,CD = a.
(1)若a =  , 求AF的长;
, 求AF的长;
(2)当a为何值时,四边形AEDF是菱形.
[基础练习]一、1. 菱形; 2. AB = AC, 或AE = AF,或AE = ED,或∠B =∠C,或DE∥AC等; 3. 5. 二、1. A; 2. D. 三、1.
[综合练习](1)菱形;(2)cm.
[探究练习](1);(2)2 ( -1).
-1).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com