2. 接着讲教科书上的例1。

在书写例1的求解过程时，可以加上“当x=7，y=4，z=0时”，以有利于弄清代数式的值的区别。本例中的代数式含有3个字母，可强调代入时一定要按照顺序进行，不要代错；代入之后，则要强调运算的顺序：在有括号的情况下，先进行括号内的运算；在进行括号内的运算时，则应遵循先乘除后加减的规定，在教科书上的两个例题中，未涉及含1个字母的代数式。实际上从函数的角度看，以后学习的函数主要还是一元函数。因此如果时间允许，可考虑在例1之后补充一个涉及1个字母的例题。

例 2当 a=2时，求代数式 　的值．

解：当 a=2时，

1. 先讲教科书第14页上的引入例，在这个涉及排球个数的代数式里，只含有一个字母。在此基础上可酌情补充一个含有两个字母的代数式的例子。

底是a厘米、高是h厘米的三角形的面积怎样表示？答：1/2ah(平方厘米)。然后，可根据这个代数式计算a，h分别取几个具体数值时的三角形的面积。

在上面例子的基础上，提出代数式的值的概念。

建议在提出代数式的值的概念后，再回到上面的例子作进一步说明。如指出当当n=15时，代数式2n+10的值是40，等等。此外，还要指出代数式与代数式的值的区别，不能笼统地说代数式的值是多少，而只能说，当字母取何值时，代数式的值是多少。

上节课学习了代数式，其目的是要通过列代数式解决问题。本课中我们学习求代数式的值，它是列代数式的一种重要应用。

　　 课本P73　 T1(2)(4)(6)(8)，4，5

　　 (1)本节课你获得了哪些知识？

(2)求代数式的值时，有哪些注意点？

P92　 习题3.3　 2、3、4

3．通过本节课的学习你收获了哪些？还有什么疑问？

2．如果给你代数式让你设计计算程序，只要严格按照有理数混合运算的运算顺序再结合设计计算框图的规范要求来设计.

(本节内容实际在复习有理数混合运算的运算顺序)

1．如果先给你计算程序，第一步把计算程序要表达的代数式表示出来.第二步实质在做求代数式值的工作.

(1) 练一练1.填表：

x	-2	-1		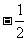0		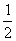1	2
2(x-3)
-5(x+1)

(2) 在下列计算程序中填写适当的数或转换步骤：