
3.用加减法解方程组 时,要使两个方程中同一未知数的系数相等或相反,有以下四种变形的结果:
时,要使两个方程中同一未知数的系数相等或相反,有以下四种变形的结果:
①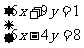 ②
② ③
③ ④
④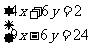
其中变形正确的是( )
A.①② B.③④ C.①③ D.②④
2. 用代入法解方程组
用代入法解方程组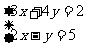 使得代入后化简比较容易的变形是( )
使得代入后化简比较容易的变形是( )
A.由①得x= B.由①得y=
B.由①得y=
C.由②得x= D.由②得y=2x-5
D.由②得y=2x-5
1. 四名学生解二元一次方程组
四名学生解二元一次方程组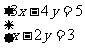 提出四种不同的解法,其中解法不正确的是( )
提出四种不同的解法,其中解法不正确的是( )
A.由①得x= ,代入② B.由①得y=
,代入② B.由①得y= ,代入②
,代入②
C.由②得y=- ,代入① D.由②得x=3+2y,代入①
,代入① D.由②得x=3+2y,代入①
教学体会:本节课通过引导学生观察方程组系数的特点,师生互动,探讨交流归纳出加减消元法,只要将相同未知量前的系数化为绝对值相等的值即可利用加减法进行消元。教学中给学生充分的探索空间,让学生通过观察、思考、尝试、交流、比较等活动,自己发现解法,体会消元化归的思想。本节效果不错,但有待进一步加强训练,以达到熟能生巧的程度。
(五)、布置作业
P89 2.(3)(4)
板书设计: 用加减法解二元一次方程组
(四)总结、扩展
1.用加减法解二元一次方程组的思想:

2.用加减法解二元一次方程组的条件:某一未知数系数绝对值相等.
3.用加减法解二元一次方程组的步骤:①变形,使某个未知数的系数绝对值相等.
②加减消元.③解一元一次方程.④代入得另一个未知数的值,从而得方程组的
(三).尝试反馈,巩固知识
练习:P89 2.(1)(2).
[教法说明]通过练习,使学生熟练地用加减法解二元一次方程组并能在练习中摸索运算技巧,培养能力.
4.变式训练,培养能力
(1)选择:二元一次方程组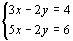 的解是( )
的解是( )
A. B.
B.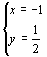 C.
C. D.
D.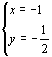
(2)已知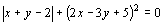 ,求
,求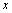 、
、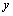 的值.
的值.
学生活动:第(1)题口答,第(2)题在练习本上完成.
[教法说明]第(1)题可以用解方程组的方法得解,也可以把四组值分别代入原方程组中,利用检验的方法解,这道题能训练学生思维的灵活性;第(2)题通过分析,学生可得方程组 从而求得
从而求得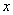 、
、 的值.此题可以培养学生分析问题,解决问题的综合能力.
的值.此题可以培养学生分析问题,解决问题的综合能力.
(二).探索新知,讲授新课
第(2)题中的第二个方程组中的两个方程中,未知数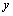 的系数有什么特点?(互为相反数)根据等式的性质,如果把这两个方程的左边与左边相加,右边与右边相加,就可以消掉
的系数有什么特点?(互为相反数)根据等式的性质,如果把这两个方程的左边与左边相加,右边与右边相加,就可以消掉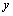 ,得到一个一元一次方程,进而求得二元一次方程
,得到一个一元一次方程,进而求得二元一次方程
组的解.
解:①+②,得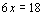
把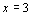 代入①,得
代入①,得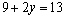
∴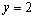
∴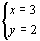
学生活动:比较用这种方法得到的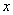 、
、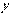 值是否与用代入法得到的相同.(相同)
值是否与用代入法得到的相同.(相同)
上面方程组的两个方程中,因为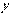 的系数互为相反数,所以我们把两个方程相加,就消去了
的系数互为相反数,所以我们把两个方程相加,就消去了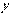 .观察一下,
.观察一下,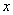 的系数有何特点?(相等)方程①和方程②经过怎样的变化可以消去
的系数有何特点?(相等)方程①和方程②经过怎样的变化可以消去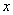 ?(相减)
?(相减)
学生活动:观察、思考,尝试用①-②消元,解方程组,比较结果是否与用①+②得到的结果相同.(相同)
我们将原方程组的两个方程相加或相减,把“二元”化成了“一元”,从而得到了方程组的解.像这种解二元一次方程组的方法叫加减消元法,简称“加减法”.
提问:①比较上面解二元一次方程组的方法,是用代入法简单,还是用加减法简单?(加减法)
②在什么条件下可以用加减法进行消元?(某一个未知数的系数相等或互为相反数)
③什么条件下用加法、什么条件下用减法?(某个未知数的系数互为相反数时用加法,系数相等时用减法)
[教法说明]这几个问题,可使学生明确使用加减法的条件,体会在某些条件下使用加减法的优越性.
例1 解方程组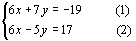
哪个未知数的系数有特点?(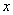 的系数相等)把这两个方程怎样变化可以消去
的系数相等)把这两个方程怎样变化可以消去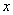 ?(相减)
?(相减)
学生活动:回答问题后,独立完成例1,一个学生板演.
解:①-②,得
∴
把 代入②,得
代入②,得
∴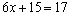
∴
∴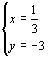
(1)检验一下,所得结果是否正确?
(2)用②-①可以消掉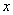 吗?(可以)是用①-②,还是用②-①计算比较简单?(①-②简单)
吗?(可以)是用①-②,还是用②-①计算比较简单?(①-②简单)
(3)把 代入①,
代入①,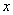 的值是多少?(
的值是多少?( ),是代入①计算简单还是代入②计算简单?(代入系数较简单的方程)
),是代入①计算简单还是代入②计算简单?(代入系数较简单的方程)
练习:P23 l.(l)(2)(3),分组练习,并把学生的解题过程在投影仪上显示.
小结:用加减法解二元一次方程组的条件是某个未知数的系数绝对值相等.
例2 解方程组
(1)上面的方程组是否符合用加减法消元的条件?(不符合)
(2)如何转化可使某个未知数系数的绝对值相等?(①×2或②×3)
归纳:如果两个方程中,未知数系数的绝对值都不相等,可以在方程两边部乘以同一个适当的数,使两个方程中有一个未知数的系数绝对值相等,然后再加减消元.
学生活动:独立解题,并把一名学生解题过程在投影仪上显示.

学生活动:总结用加减法解二元一次方程组的步骤.
①变形,使某个未知数的系数绝对值相等.
②加减消元.
③解一元一次方程.
④代入得另一个未知数的值,从而得方程组的解.
Ⅰ明确目标:
本节课通过复习代入法从而引入另一种消元的办法,即加减法解二元一次方程组.
Ⅱ整体感知:
加减法解二元一次方程组的关键在于将相同字母的系数化为绝对值相等的值,即可使用加减法消元.故在教学中应反复教会学生观察并抓住解题的特征及办法从而方便解题.
Ⅲ过程设计:
(-)创设情境,复习导入
(1)用代入法解二元一次方程组的基本思想是什么?
(2)用代入法解下列方程组,并检验所得结果是否正确.

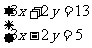
学生活动:口答第(1)题,在练习本上完成第(2)题,一个同学说出结果.
上面的方程组中,我们用代入法消去了一个未知数,将“二元”转化为“一元”,从而得到了方程组的解.对于二元一次方程组,是否存在其他方法,也可以消去一个未知数,达到化“二元”为“一元”的目的呢?这就是我们这节课将要学习的内容.
[教法说明]由练习导入新课,既复习了旧知识,又引出了新课题,教学过程中还可以进行代入法和加减法的对比,训练学生根据题目的特点选取适当的方法解题.
3.通过反复的训练、归纳、再训练、再归纳,从而积累用加减法解方程组的经验,进而上升到理论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com