
数学教学是数学活动的教学,是师生之间、学生之间交往互动与共同参与发展的过程。本节课的评价要让学生体会到参与学习、与人合作的重要性,获得成绩的喜悦,从而激发性的学习动力。在这节的数学课,如要获得最直接、真实的反馈,就要尽量让学生多说、多思考,对于学生提出的问题和解决问题的方法,教师都要给予鼓励和引导,并随时观察解决,评价应充分考虑到每个学生的差异,这节课通过现代化的技术的运用,节省出尽可能多的时间,提出挑战性的问题,让学生通过开放式的数学讨论提高学生学习的兴趣,在交流中获益。通过随堂练习和作业来激励其学习。同时做练习时,将评价及时反馈给学生,树立学习数学的自信心,促进学生的进一步发展。并在课后作成长记录,使学生比较全面了解自己的学习过程,特别感受自己的不断成长和进步,为下一步教学提供重要依据。
3、通过交流,让学生用自己的语言清楚地表达解决问题的过程,提高学生的语言表达能力·
活动2
下面方程 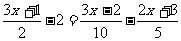 可以怎样求解?
可以怎样求解?
观察方程,回答教师提出的问题并对学生的回答进行总结:先去分母·
怎样去分母?
解去掉分母后的这个方程
归纳总结去分母的方法:在方程两边同时乘以所有分母的最小公倍数;依据是等式的性质2,即"等式两边同时乘同一个数,结果仍相等·"
呈现不同学生的解题过程,选取学生在去分母过程中出现的典型错误,引导全体学生共同分析错误的原因,发现去分母的易错点·巩固了学生对解方程的透彻理解。这样做的目的不仅培养了学生的学习自主性和团体协作精神,还对与重、难点知识的突破起到了一定的促进作用。
通过对错例的辨析,加深学生对 "去分母"的认识,避免解方程时出现类似错误·
去掉分母后,方程即转化为熟悉的形式,新旧知识自然衔接,使学生体会到,只要把
新问题想办法合理转化为熟悉的知识,问题就能得以解决通过在解方程过程中"去分母"这一步骤体会转化思想·
活动3 解方程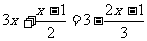
设计意图:用实践来加深对 "去分母"的方法解一元一次方程的认识· 结合本题思考,能总结解这种方程的一般操作过程吗?
巩固所学的一元一次方程的解法,同时说明解方程的步骤是程序化的,但不能生搬硬
套,每个步骤要不要使用、何时使用都应视方程的特征而定·了解对方程的每一次变形都是为了将方程最终化归为的形式·解题时应根据题目特点,合理选择解题步骤·
小结
活动4总结
(1)学生能否总结本节的知识,是否理解去分母的作用、依据,是否掌握去分母的具体做法;
(2)学生是否掌握了一元一次方程解法的一般步骤;
(3)学生是否能准确表达自己的观点·
最后复习、巩固本节的知识,学会总结反思·
教学活动流程图 活动内容和目的
 活动1列方程解决实际问题 创设埃及古题问题情境,列方程解决该问题;发展利用方程方法解决简单实际问题的能力,再次感受方程是刻画现实世界量与量之间关系的主要模型之一·
活动1列方程解决实际问题 创设埃及古题问题情境,列方程解决该问题;发展利用方程方法解决简单实际问题的能力,再次感受方程是刻画现实世界量与量之间关系的主要模型之一·
 活动2解含有分母的一元一次方程
以学生已有的关于等式性质的数学知识基础,探索利用“去分母"的方法解一元一次方程·
活动2解含有分母的一元一次方程
以学生已有的关于等式性质的数学知识基础,探索利用“去分母"的方法解一元一次方程·
 活动3 "去分母"的方法解一元一次方程
用"去分母"的方法解一元一次方程,掌握 "去分母"的方法解一元一次方程应注意的事项;归纳一元一次方程解法的一般步骤·
活动3 "去分母"的方法解一元一次方程
用"去分母"的方法解一元一次方程,掌握 "去分母"的方法解一元一次方程应注意的事项;归纳一元一次方程解法的一般步骤·
 活动4 小结
总结本节收获
活动4 小结
总结本节收获
活动1、创设问题情境:
引言:这件珍贵的文物是纸莎草文书, 是古代埃及人用象形文字写在一种特殊的草上的著作,至今已有3700多年的历史了·在文书中记载了许多有关数学的问题·
问题 一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33。
(1)能不能用方程解决这个问题?
(2)能尝试解这个方程吗? (3)不同的解法有什么各自的特点?
设计意图:1、利用列方程、解方程解决实际问题,再一次让学生感受方程的优越性,提高学生主动使用方程的意识·
2、经过对同一方程不同解法到去分母能够使解方程的过程更加便捷,明白为什么要去分母,这是 "去分母"这一步骤的必要性;同时,让学生认同"去分母"是科学的、可行的,明确为什么能去分母·这样,学生就会自觉参与探索去分母的一般做法的活动,从而发现"方程两边同时乘以所有分母的最小公倍数"这一方法·也首次由学生自行突破了难点。
在前面的学段中,学生已学习了合并同类项、去括号等整式运算内容。解一元一次方程就成为承上启下的重要内容。因此,它既是重点也是难点。我根据学生认识规律和教学的启发性、直观性和面向全体因材施教等教学原则,积极创设新颖的问题情境,以“学生发展为本,以活动为主线,以创新为主旨”,采用多媒体教学等有效手段,以引导法为主,辅之以直观演示法、讨论法,向学生提供充分从事数学活动的机会,激发学生的学习积极性,使学生主动参与学习的全过程。
我的教学设计的指导思想是: 1、让学生自己去尝试发现问题,而不是被动的回答老师的问题、接受老师的答案。3、精心设计问题,因为好的问题设计能不断激发学习动机,还能给学生提供学习的目标和思维的空间,使学生自主学习真正成为可能。授课中通过一系列层层递进的问题,给学生充分的时间和广阔的思维空间,充分表达自己的想法,在此基础上解决问题并得出结论。
3、教学难点:探究通过"去分母"的方法解一元一次方程
2、教学重点:通过"去分母"解一元一次方程
2、通过埃及古题的情境感受数学文明.
2、了解一元一次方程解法的一般步骤·
(2)、能力目标: 经历 "把实际问题抽象为方程"的过程,发展用方程方法分析问题、解决问题的能力,
(3)、情感目标:1、通过具体情境引入新问题(如何去分母),激发学生的探究欲望
方程是应用非常广泛的数学工具,它在义务教育阶段的数学课程中占重要地位。本节课的教学内容是《解一元一次方程》的第3课时。解方程既是本章的重点也为今后学习其他方程、不等式及函数有重要基础作用。为了使学生牢固掌握解方程体会方程是刻画现实世界的一个有效的数学模型,产生学习解方程的欲望,教材设置了新颖的问题情境,让学生从具体的情境中获取信息,列方程,然后尝试主动探究方程的解法。并通过练习归纳掌握解方程的基本步骤和技能。
1、教 学 目 标
(1)、知识目标:1、掌握解一元一次方程中"去分母"的方法,并能解这种类型的方程·
23、(6分)某自行车厂今年生产销售一种新型自行车,现向你提供以下有关信息:(1)该厂去年已备有这种自行车车轮10000只,车轮车间今年平均每月可生产车轮1500只,每辆自行车需装配2只车轮;(2)该厂装配车间(自行车最后一道工序的生产车间)每月至少可装配这种自行车1000辆,但不超过1200辆;(3)该厂已收到各地客户今年订购这种自行车共14500辆自行车的订货单;(4)这种自行车出厂销售单价为500元/辆。设该厂今年这种自行车的销售金额为a万元。请你根据上述信息,判断a的取值范围是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com