
14. 证明:连接AF,AE
∵
∴∠AFB= ∠EAQ
同理可证:∠FAP= ∠AEQ
又∵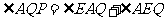 ,
,
∴∠AQP= ∠APQ
∴AP= AQ, △APQ为等腰三角形。
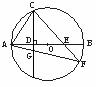
13. 解:连接AO并延长,交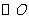 于点D,连接BD.
于点D,连接BD.
 ∵AD为
∵AD为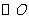 的直径
的直径
∴
又∵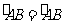
∴
∴
∴
∴OA=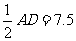
∴ 的半径长为7.5
的半径长为7.5
12. (1)相等.理由如下:连接OD,∵AB⊥CD,AB是直径,
∴ ,∴∠COB= ∠DOB.
,∴∠COB= ∠DOB.
∵∠COD=2∠P,∴∠COB=∠P,即∠COB=∠CPD.
(2)∠CP′D+∠COB=180°.
理由如下:连接P′P,
则∠P′CD=∠P′PD,∠P′PC=∠P′DC.
∴∠P′CD+∠P′DC=∠P′PD+∠P′PC=∠CPD.
∴∠CP′D=180°-(∠P′CD+∠P′DC)=180°-∠CPD=180°-∠COB,
从而∠CP′D+∠COB=180°.
11.提示:连接AB、BC,作两线段的垂直平分线,两垂直平分线的交点既为所求。作图略。
11.已知,如图,AB是⊙O的直径,C是⊙O上一点,连接AC,过点C作直线CD⊥AB于D(AD<DB),点E是DB上任意一点(点D、B除外),直线CE交⊙O于点F,连接AF与直线CD交于点G.
(1)求证:AC2=AG·AF;
(2)若点E是AD(点A除外)上任意一点,上述结论是否仍然成立?若成立,请画出图形并给予证明;若不成立,请说明理由.
答案与提示
基础训练
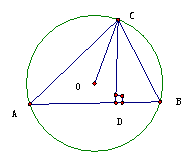
10. 如图,△ABC内接于 ,CD是AB边上的高,试探究∠ACO和 ∠BCD的大小关系。
,CD是AB边上的高,试探究∠ACO和 ∠BCD的大小关系。
9. 图9是破残的圆轮片,现想把它复原成与原物大小相同的圆轮,你的方案怎样?请在图中用尺规作图补全图形.(不写作法,保留作图痕迹)

图9
.
8.(2006 吉林课改)如图,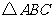 是
是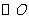 的内接三角形,
的内接三角形, ,点
,点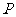 在
在 上移动(点
上移动(点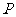 不与点
不与点 ,
,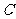 重合),则
重合),则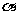 的变化范围是_______.
的变化范围是_______.
7. (2005 南宁课改)如图,在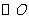 中,
中, .则
.则 的度数为 .
的度数为 .


6.如图2,⊙O的直径AC=2,∠BAD=75°,∠ACD=45°,则四边形ABCD的周长为_____(结果取准确值).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com