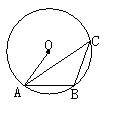
4.如图4,A、B、C为⊙O上三点，若∠OAB=46°,则∠ACB=_______度.

　　　 (4)　　　　　　　　 (5)　　　　　　　　　　　 (6)

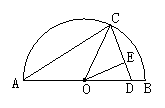
3.已知,如图3,∠BAC的对角∠BAD=100°,则∠BOC=_______度.

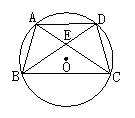
2.如图2,四边形ABCD的四个顶点都在⊙O上,且AD∥BC,对角线AC与BC相交于点E,那么图中有_________对全等三角形;________对相似比不等于1的相似三角形.

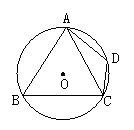
1.如图1,等边三角形ABC的三个顶点都在⊙O上,D是上任一点(不与A、C重合),则∠ADC的度数是________.毛

　　　 (1)　　　　　　　　 (2)　　　　　　　　 (3)

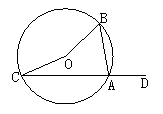
11. (1)证明：连接CB，∵AB是直径，CD⊥AB, ∴∠ACB=∠ADC=90°. ∴Rt△CAD∽Rt△BAC.

∴得∠ACD=∠ABC .　 ∵∠ABC=∠AFC, ∴∠ACD=∠AFC.　 ∴△ACG∽△ACF.

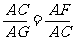∴.　 ∴AC²=AG·AF.

(2)当点E是AD(点A除外)上任意一点，上述结论仍成立

①当点E与点D重合时，F与G重合,

有AG=AF，∵CD⊥AB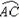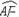，∴=, AC=AF. ∴AC²=AG·AF.

②当点E与点D不重合时(不含点A)时，证明类似①.

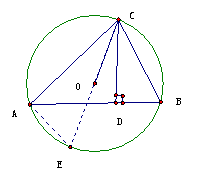
10. 解：∠ACO= ∠BCD

证明：延长CO交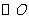于E，连接AE.

∵CE是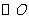的直径,

∴∠CAE=90⁰

又∵CD⊥AB

∴∠BDC=90⁰,

∴∠CAE=∠BDC.

又∠E，∠ B是同弧上的圆周角,

∴∠E=∠B，

∴

∴∠ACO= ∠BCD

9. 在圆轮片边沿任取三点，依次连接两点成两条线段；作两线段的垂直平分线，则两垂直平分线的交点即为圆心，再以圆心与所取三点中任意一点线段长为半径作圆，此圆即为残圆轮的复原圆.　　 (图略)

4. 答案：D。连接BC，则有，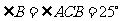

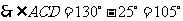
3. 答案：A.利用垂径定理或构造直径，借助直角三角形求解。易错点：同弦所对的两个圆周角相等或互补。

15. 四边形AFDE是菱形.

证明：∵AB=AC

∴∠ABC=∠ACB,

又∵BE、CF分别平分∠ABC和∠ACB,

∴∠ABE=∠EBC=∠ACF=∠FCB.

又∠FAB，∠FCB是同弧上的圆周角,

∴∠FAB=∠FCB，同理∠EAC=∠EBC.

有∠FAB=∠ABE=∠EAC=∠ACF.

∴AF∥ED，AE∥FD

又∵∠ABE =∠ACF.

∴

∴AF=AE.

∴四边形AFDE是菱形.

能力提高