P97　 习题3.4　 2

(1) 本节课你学到了哪些知识? (生: 同类项,合并同类项)

(2) 请你举例说明同类项.

(3) 举例说明怎样合并同类项.

5．练一练：P96

4. 例1：合并同类项：

(1)-3x+2y-5x-7y；

解：-3x+2y-5x-7y

=(-3x-5x)+(2y-7y)　　 加法交换律

=(-3-5)x+(2-7)y　　　 合并同类项法则、有理数加法法则

=-8x-5y

(括号内的说理,只在课堂上结合具体的计算进行口头训练,对学生的课外作业不必这样要求.)

(2)a²-3ab+5-a²-3ab-7

解：a²-3ab+5-a²-3ab-7

　 =(a²-a²)+(-3ab-3ab)+(5-7)

　 =(1-1)a²+(-3-3)ab+(-2)

　 =-6ab-2

3. 做一做：把下列各式的同类项合并成一项，并说出你计算的理由：

(1)　 7a -3a=

(2)　 4x²+2x²=

(3)　 5ab²-13ab²=

(4)　 -9x²y³+5x²y³=

(学生先“做“，在“做”中不断感受，再明晰法则。其意图是引导学生经历“从感性到理性”的认识过程，更好地理解、掌握合并同类项法则。)

把同类项合并成一项叫做合并同类项

揭示合并同类项的法则：同类项的系数相加，所得的结果作为系数，字母和字母的指数不变。

2. 揭示定义：

所含字母相同，并且相同字母的指数相同，向这样的项是同类项。

1. 议一议：

100a 和200a 、240b 和60b 、5ab²和-13ab²、-9x²y³和5x²y³有什么共同特点？

1)所含字母相同

2)相同字母的指数相同

2.下图为某学校校园的总体规划图(单位：m)，试计算这个学校的占地面积。

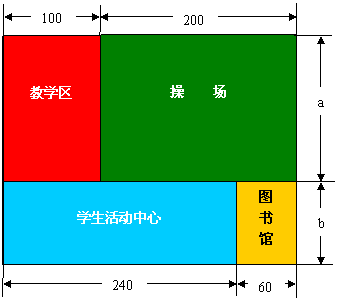
小丽说：学校的占地面积可以用代数式表示为100a+200a+240b+60b

小明说：也可以表示为(100+200)a+(240+60)b

可以看出：100a+200a+240b+60b=(100+200)a+(240+60)b

由此可知：计算100a+200a，可以先把它们的系数相加，再乘a；

　　　　　 计算240b+60b，可以先把它们的系数相加，再乘b。

引入新课：这节课我们就来学习3.4合并同类项

1.星期天，小明上街买了4个苹果，8个橘子，7个香蕉。妈妈不知道小明已经买了水果，于是，下班后妈妈从街上又买来5个苹果 ，10个橘子，6个香蕉，问：苹果，橘子，香蕉一共各有多少个？

生：4个苹果 + 5个苹果 = 9个苹果

8个橘子 + 10个橘子 = 18个橘子

7个香蕉 + 6个香蕉 = 13个香蕉

师：你们是根据什么来求和的？(引导学生说出苹果是一类，橘子是一类，香蕉是一类)

6.作业：见作业本。