
28.有一火车以每分钟600米的速度要过完第一、第二两座铁桥,过第二铁桥比过第一铁桥需多5秒,又知第二铁桥的长度比第一铁桥长度的2倍短50米,试求各铁桥的长.
解:设第一铁桥的长为x米,那么第二铁桥的长为(2x-50)米,过完第一铁桥所需的时间为 分.过完第二铁桥所需的时间为
分.过完第二铁桥所需的时间为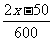 分.依题意,可列出方程
分.依题意,可列出方程
 +
+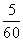 =
=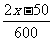 解方程x+50=2x-50 得x=100
解方程x+50=2x-50 得x=100
∴2x-50=2×100-50=150
答:第一铁桥长100米,第二铁桥长150米.
27.长方体甲的长、宽、高分别为260mm,150mm,325mm,长方体乙的底面积为130×130mm2,又知甲的体积是乙的体积的2.5倍,求乙的高?
设乙的高为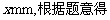
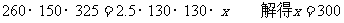
知能点6:行程问题
基本量之间的关系: 路程=速度×时间 时间=路程÷速度 速度=路程÷时间
(1)相遇问题 (2)追及问题
快行距+慢行距=原距 快行距-慢行距=原距
(3)航行问题
顺水(风)速度=静水(风)速度+水流(风)速度
逆水(风)速度=静水(风)速度-水流(风)速度
抓住两码头间距离不变,水流速和船速(静不速)不变的特点考虑相等关系.
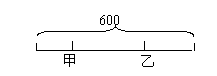
例6. 甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
(1)慢车先开出1小时,快车再开。两车相向而行。问快车开出多少小时后两车相遇?
(2)两车同时开出,相背而行多少小时后两车相距600公里?
(3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600公里?
(4)两车同时开出同向而行,快车在慢车的后面,多少小时后快车追上慢车?
(5)慢车开出1小时后两车同向而行,快车在慢车后面,快车开出后多少小时追上慢车?
此题关键是要理解清楚相向、相背、同向等的含义,弄清行驶过程。故可结合图形分析。
 (1)分析:相遇问题,画图表示为:
(1)分析:相遇问题,画图表示为:
等量关系是:慢车走的路程+快车走的路程=480公里。
解:设快车开出x小时后两车相遇,由题意得,140x+90(x+1)=480 解这个方程,230x=390
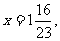
答:快车开出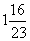 小时两车相遇
小时两车相遇
分析:相背而行,画图表示为:
等量关系是:两车所走的路程和+480公里=600公里。
解:设x小时后两车相距600公里,
由题意得,(140+90)x+480=600解这个方程,230x=120 ∴ x= 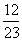
答: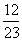 小时后两车相距600公里。
小时后两车相距600公里。
(3)分析:等量关系为:快车所走路程-慢车所走路程+480公里=600公里。
解:设x小时后两车相距600公里,由题意得,(140-90)x+480=600 50x=120 ∴ x=2.4
 答:2.4小时后两车相距600公里。
答:2.4小时后两车相距600公里。
分析:追及问题,画图表示为:
等量关系为:快车的路程=慢车走的路程+480公里。
解:设x小时后快车追上慢车。
由题意得,140x=90x+480 解这个方程,50x=480 ∴ x=9.6
答:9.6小时后快车追上慢车。
分析:追及问题,等量关系为:快车的路程=慢车走的路程+480公里。
解:设快车开出x小时后追上慢车。由题意得,140x=90(x+1)+480 50x=570 ∴ x=11.4
答:快车开出11.4小时后追上慢车。
例7. 甲乙两人在同一道路上从相距5千米的A、B两地同向而行,甲的速度为5千米/小时,乙的速度为3千米/小时,甲带着一只狗,当甲追乙时,狗先追上乙,再返回遇上甲,再返回追上乙,依次反复,直至甲追上乙为止,已知狗的速度为15千米/小时,求此过程中,狗跑的总路程是多少?
[分析]]追击问题,不能直接求出狗的总路程,但间接的问题转化成甲乙两人的追击问题。狗跑的总路程=它的速度×时间,而它用的总时间就是甲追上乙的时间
解:设甲用X小时追上乙,根据题意列方程
5X=3X+5 解得X=2.5,狗的总路程:15×2.5=37.5
答:狗的总路程是37.5千米。
例8. 某船从A地顺流而下到达B地,然后逆流返回,到达A、B两地之间的C地,一共航行了7小时,已知此船在静水中的速度为8千米/时,水流速度为2千米/时。A、C两地之间的路程为10千米,求A、B两地之间的路程。
[分析]这属于行船问题,这类问题中要弄清:
(1)顺水速度=船在静水中的速度+水流速度;
(2)逆水速度=船在静水中的速度-水流速度。相等关系为:顺流航行的时间+逆流航行的时间=7小时。
解:设A、B两码头之间的航程为x千米,则B、C间的航程为(x-10)千米,
由题意得,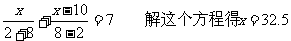
答:A、B两地之间的路程为32.5千米。
26.一个装满水的内部长、宽、高分别为300毫米,300毫米和80毫米的长方体铁盒中的水,倒入一个内径为200毫米的圆柱形水桶中,正好倒满,求圆柱形水桶的高(精确到0.1毫米,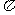 ≈3.14).
≈3.14).
解:设圆柱形水桶的高为x毫米,依题意,得 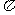 ·(
·(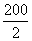 )2x=300×300×80
)2x=300×300×80
x≈229.3
答:圆柱形水桶的高约为229.3毫米.
25.某粮库装粮食,第一个仓库是第二个仓库存粮的3倍,如果从第一个仓库中取出20吨放入第二个仓库中,第二个仓库中的粮食是第一个中的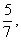 问每个仓库各有多少 粮食?
问每个仓库各有多少 粮食?
设第二个仓库存粮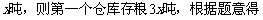

(2)等积变形问题
常见几何图形的面积、体积、周长计算公式,依据形虽变,但体积不变.
①圆柱体的体积公式
V=底面积×高=S·h=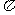 r2h
r2h
②长方体的体积
V=长×宽×高=abc
24.一项工程甲单独做需要10天,乙需要12天,丙单独做需要15天,甲、丙先做3天后,甲因事离去,乙参与工作,问还需几天完成?
设还需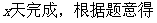

知能点5:若干应用问题等量关系的规律
(1)和、差、倍、分问题 此类题既可有示运算关系,又可表示相等关系,要结合题意特别注意题目中的关键词语的含义,如相等、和差、几倍、几分之几、多、少、快、慢等,它们能指导我们正确地列出代数式或方程式。 增长量=原有量×增长率 现在量=原有量+增长量
22.一批工业最新动态信息输入管理储存网络,甲独做需6小时,乙独做需4小时,甲先做30分钟,然后甲、乙一起做,则甲、乙一起做还需多少小时才能完成工作?
解:设甲、乙一起做还需x小时才能完成工作.
根据题意,得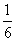 ×
×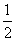 +(
+(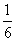 +
+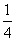 )x=1 解这个方程,得x=
)x=1 解这个方程,得x=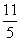
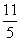 =2小时12分
=2小时12分
答:甲、乙一起做还需2小时12分才能完成工作.
23某车间有16名工人,每人每天可加工甲种零件5个或乙种零件4个.在这16名工人中,一部分人加工甲种零件,其余的加工乙种零件.已知每加工一个甲种零件可获利16元,每加工一个乙种零件可获利24元.若此车间一共获利1440元,求这一天有几个工人加工甲种零件.
解:设这一天有x名工人加工甲种零件,则这天加工甲种零件有5x个,乙种零件有4(16-x)个. 根据题意,得16×5x+24×4(16-x)=1440 解得x=6
答:这一天有6名工人加工甲种零件.
21.购买了25000元某公司1年期的债券,一年后扣除20%的利息税之后得到本息和为26000元,这种债券的年利率是多少?答案:百分之五
知能点4:工程问题
工作量=工作效率×工作时间 工作效率=工作量÷工作时间
工作时间=工作量÷工作效率 完成某项任务的各工作量的和=总工作量=1
例5. 一件工作,甲独作10天完成,乙独作8天完成,两人合作几天完成?
[分析]甲独作10天完成,说明的他的工作效率是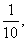 乙的工作效率是
乙的工作效率是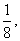
等量关系是:甲乙合作的效率×合作的时间=1
解:设合作X天完成, 依题意得方程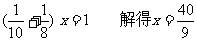
答:两人合作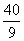 天完成
天完成
例6. 一件工程,甲独做需15天完成,乙独做需12天完成,现先由甲、乙合作3天后,甲有其他任务,剩下工程由乙单独完成,问乙还要几天才能完成全部工程?
[分析]设工程总量为单位1,等量关系为:甲完成工作量+乙完成工作量=工作总量。
解:设乙还需x天完成全部工程,设工作总量为单位1,由题意得,
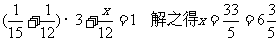
答:乙还需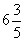 天才能完成全部工程。
天才能完成全部工程。
例7. 一个蓄水池有甲、乙两个进水管和一个丙排水管,单独开甲管6小时可注满水池;单独开乙管8小时可注满水池,单独开丙管9小时可将满池水排空,若先将甲、乙管同时开放2小时,然后打开丙管,问打开丙管后几小时可注满水池?
[分析]等量关系为:甲注水量+乙注水量-丙排水量=1。
解:设打开丙管后x小时可注满水池,
由题意得,
答:打开丙管后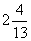 小时可注满水池。
小时可注满水池。
20.用若干元人民币购买了一种年利率为10% 的一年期债券,到期后他取出本金的一半用作购物,剩下的一半和所得的利息又全部买了这种一年期债券(利率不变),到期后得本息和1320元。问张叔叔当初购买这咱债券花了多少元?答案:22000元
19.某人按定期2年向银行储蓄1500元,假设每年利率为3%(不计复利)到期支取时,扣除利息所得税(税率为20%)此人实得利息为( )
A、1272元 B、36元 C、72元 D、1572元
18.(北京海淀区)白云商场购进某种商品的进价是每件8元,销售价是每件10元(销售价与进价的差价2元就是卖出一件商品所获得的利润).现为了扩大销售量,把每件的销售价降低x%出售,但要求卖出一件商品所获得的利润是降价前所获得的利润的90%,则x应等于( ).
A.1 B.1.8 C.2 D.10
C [点拨:根据题意列方程,得(10-8)×90%=10(1-x%)-8,解得x=2,故选C]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com