4.三个连续偶数的和为72,设中间一个为2n,可列方程为___________ .

3.甲、乙两数的和为10，并且甲比乙大2，求甲、乙两数？下面列式正确的是(　 ).

A.　　 设乙数为x,则(x+2)+x＝10

B.　　 设乙数为x，则(x-2)+x＝10

C.　　 设甲数为x，则(x+2)+x＝10

D.　　 设甲数为x，则x-2＝10

2.七年级有甲、乙两个班，甲班有43人，乙班有49人，要使两班人数相等，应从乙班调(　　 )人到甲班.

A.6人　　　　　　 B.5人　　　　　　 C.4人　　　　　　　　 D.3人.

1. 某数的5倍减去4比该数的6倍大1，求某数x可列方程(　 )

A.5x-4=6x-1 B. 5x-4=6x+1　 C. 5x+4=6x+1 D. 5x-4=6x-1

学生在比较探究后发现用方法二较简便。

设问1：如果选择方法二，如何计算平均每只母牛和每只小牛1天各约需用饲料量？

(有前面几节的知识准备，学生可以回答)

列方程组求解。

主要思路：

实际问题→(设未知数，列方程组)→数学问题(二元一次方程组)

学生先独立思考，然后师生共同讨论解题过程。

解：设平均每只母牛和每只小牛1天各约需用饲料x kg和y kg。

找出相等关系列方程组

解这个方程组，得

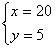
这就是说，平均每只母牛和每只小牛1天各约需用饲料20kg和5kg。饲养员李大叔对母牛的食量估计正确，对小牛的食量估计不正确。

引导学生探寻解题思路，并对各种方法进行比较，方法一主要是估算的运用，而方法二是方程思想的应用。

分步到位，渗透模型化的思想。

规范解题步骤，培养学生有条理地思考、表达的习惯。

让学生认识到检验的重要性，并学会正确作答。

拓广探索，比较分析

　设问2：以上问题还能列出不同的方程组吗？结果是否一致？

个别学生可能会列出如下方程组

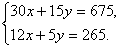
但结果一致。

比较分析，加深对方程组的认识。

课堂练习，反馈调控

　《一千零一夜》中有这样一段文字：有一群鸽子，其中一部分在树上欢歌，另一部分在地上觅食。树上的一只鸽子对地上觅食的鸽子说：“若从你们中飞上来一只，则树下的鸽子就是整个鸽群的1/3；若从树上飞下去一只，则树上、树下的鸽子就一样多了。”你知道树上、树下各有多少只鸽子吗？

教师巡视、指导，师生共同讲评。　

出示古典名题，一方面及时巩固用方程组解决实际问题的过程，另一方面让学生感受数学文化。

课堂小结，知识梳理

提问：通过这节课的学习，你知道用方程组解决实际问题有哪些步骤？

学生思考后回答、整理：

　①设未知数。

　②找相等关系。

　③列方程组。

　④检验并作答。

以问题的形式出现，引导学生思考、交流，梳理所学知识，建立起符合自身认识特点的知识结构。

训练口头表达能力，养成及时归纳总结的良好学习习惯。

布置作业，自我评价

　①必做题：课本第116页习题8．3第1(1)、3、5题。

　②选做题：课本第117页习题8．3第8题。

　③备选题：

　(1)解方程组：

　(2)据《新华日报》消息，巴西医生马廷恩经过10年苦心研究后得出结论：卷入腐败行为的人容易得癌症、心肌梗塞、过敏症、脑溢血、心脏病等。如果将犯有贪污受贿的580官员与600名廉洁官员进行比较，可发现，后者的健康人数多272名，两者患病(致死)者共有444人，试问犯有贪污受贿罪的官员与廉洁官员的健康人数各占百分之几？

　(3)《希腊文集》中有一些用童话形式写成的数学题。比如“驴和骡子驮货物”这道题，就曾经被大数学家欧拉改编过。题目是这样的：“驴和骡子驮着货物并排走在路上。驴不住地埋怨自己驮的货物太重，压得受不了。骡子对驴说：‘你发什么牢骚啊！我驮的货物比你重。假若你的货物给我一口袋，我驮的货就比你驮的重一倍，而我若给你一口袋，咱俩驮的才一样多。’问驴和骡子各驮几口袋货物？”

　你能用方程组来解这个问题吗？　

　为满足不同学生的发展需求，在保证基本要求的同时，为更多有数学学习需求的学生提供机会和资料，分层次布置作业。备选题供教师参考。

　从实际问题出发，通过分析实际问题中的数量关系，列出二元一次方程组这种数学模型，通过对方程组解的检验，让学生认识到检验不仅要检查求得的解是否适合方程组中的每一个方程，而且还要考查所得的解答是否符合实际问题的要求，初步体验用方程组解决实际问题的全过程。

　在重视方程的应用价值的同时关注其文化内涵。给出《一千零一夜》《希腊文集》中的数学名题，使学生在数学知识和能力得到提高的同时能够感受到数学文化的熏陶。

本案例选自延边教育出版社《课堂教学设计与案例》新课标教

33．一个两位数，十位数与个位上的数字之和为11，如果把十位上的数字与个位上的数字对调，那么得到的数比原来的数大63，求原来的两位数？

设个位数字为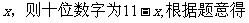

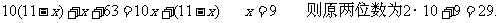
注意：虽然我们分了几种类型对应用题进行了研究，但实际生活中的问题是千变万化的，远不止这几类问题。因此我们要想学好列方程解应用题，就要学会观察事物，关心日常生产生活中的各种问题，如市场经济问题等等，要会具体情况具体分析，灵活运用所学知识，认真审题，适当设元，寻找等量关系，从而列出方程，解出方程，使问题得解。

32．一轮船在甲、乙两码头之间航行，顺水航行需要4小时，逆水航行需要5小时，水流的速度为2千米/时，求甲、乙两码头之间的距离。

知能点7：数字问题

(1)要搞清楚数的表示方法：一个三位数的百位数字为a，十位数字是b，个位数字为c(其中a、b、c均为整数，且1≤a≤9， 0≤b≤9， 0≤c≤9)则这个三位数表示为：100a+10b+c。然后抓住数字间或新数、原数之间的关系找等量关系列方程．

(2)数字问题中一些表示：两个连续整数之间的关系，较大的比较小的大1；偶数用2n表示，连续的偶数用2n+2或2n-2表示；奇数用2n+1或2n-1表示。

例1. 一个三位数，三个数位上的数字之和是17，百位上的数比十位上的数大7，个位上的数是十位上的数的3倍，求这个三位数

[分析]由已知条件给出了百位和个位上的数的关系，若设十位上的数为x，则百位上的数为X+7，个位上的数是3X，等量关系为三个数位上的数字和为17。

解：设这个三位数十位上的数为X，则百位上的数为X+7，个位上的数是3X

X+X+7+3X=17　　　 解得X=2

X+7=9，3X=6　 答：这个三位数是926

例2. 一个两位数，个位上的数是十位上的数的2倍，如果把十位与个位上的数对调，那么所得的两位数比原两位数大36，求原来的两位数

等量关系：原两位数+36=对调后新两位数

解：设十位上的数字X，则个位上的数是2X，

10×2X+X=(10X+2X)+36解得X=4，2X=8，答：原来的两位数是48。

31．一架飞机在两个城市之间飞行，风速为24千米/小时，顺风飞行需要2小时50分，逆风飞行需要3小时，求两个城市之间的飞行路程？

设两个城市之间的飞行路程为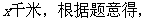

30．一队学生去军事训练，走到半路，队长有事要从队头通知到队尾，通讯员以18米/分的速度从队头至队尾又返回，已知队伍的行进速度为14米/分。问：若已知队长320米，则通讯员几分钟返回？‚若已知通讯员用了25分钟，则队长为多少米？

(1)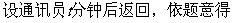　　　　　　 (2)

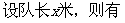
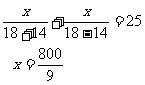
29．已知甲、乙两地相距120千米，乙的速度比甲每小时快1千米，甲先从A地出发2小时后，乙从B地出发，与甲相向而行经过10小时后相遇，求甲乙的速度？

设甲的速度为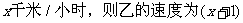千米/小时，依题意得，