6．工程问题

　　 工作量＝工作效率×工作时间

　　 工作效率＝工作量÷工作时间

　　 工作时间＝工作量÷工作效率

　　 完成某项任务的各工作量的和＝总工作量＝1

5．行程问题

　　 基本量之间的关系

　　 路程＝速度×时间

　　 时间＝路程÷速度

　　 速度＝路程÷时间

　 (1)相遇问题

　　 快行距+慢行距＝原距

　 (2)追及问题

　　 快行距－慢行距＝原距

　 (3)航行问题

　　 顺水(风)速度＝静水(风)速度+水流(风)速度

　　 逆水(风)速度＝静水(风)速度－水流(风)速度

　　 抓住两码头间距离不变，水流速和船速(静不速)不变的特点考虑相等关系．

4．市场经济问题

　 (1)商品利润＝商品售价－商品成本价

　 (2)商品利润率＝×100%

　 (3)商品销售额＝商品销售价×商品销售量

　 (4)商品的销售利润＝(销售价－成本价)×销售量

　 (5)商品打几折出售，就是按原标价的百分之几十出售，如商品打8折出售，即按原标价的80%出售．

3．数字问题

　　 一般可设个位数字为a，十位数字为b，百位数字为c．

　　 十位数可表示为10b+a，

　　 百位数可表示为100c+10b+a．

　 　然后抓住数字间或新数、原数之间的关系找等量关系列方程．

2．若干应用问题等量关系的规律

　 (1)和、差、倍、分问题

　　 增长量＝原有量×增长率

　　 现在量＝原有量+增长量

　 (2)等积变形问题

　　 常见几何图形的面积、体积、周长计算公式，依据形虽变，但体积不变．

　　 ①圆柱体的体积公式

　　 V=底面积×高＝S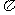·h＝r²h

　　 ②长方体的体积

　　 V＝长×宽×高＝abc

1．列一元一次方程解应用题的一般步骤

　　 (1)审题：弄清题意．

　　 (2)找出等量关系：找出能够表示本题含义的相等关系．

　　 (3)设出未知数，列出方程：设出未知数后，表示出有关的含字母的式子，然后利用已找出的等量关系列出方程．

　　 (4)解方程：解所列的方程，求出未知数的值．

　　 (5)检验，写答案：检验所求出的未知数的值是否是方程的解，是否符合实际，检验后写出答案．

3.4实际问题与一元一次方程(2)同步精练

◆阶段性内容回顾

13．(北京海淀区)白云商场购进某种商品的进价是每件8元，销售价是每件10元(销售价与进价的差价2元就是卖出一件商品所获得的利润)．现为了扩大销售量，把每件的销售价降低x%出售，但要求卖出一件商品所获得的利润是降价前所获得的利润的90%，则x应等于(　 )．

　　 A．1　　　 B．1.8　　　 C．2　　　　 D．10

12．请同学们对以下情境提出问题，并讨论解答(必要时可对情境作适当补充)：

　　 某校七年级(2)班组织去风景区旅游，大部分同学先坐公共汽车前往，平均速度为26千米/时；5名负责后勤的同学晚半小时坐学校汽车出发，速度为60千米/时，同时到脚下．到达后发现乘坐缆车上山费用较大，且不能浏览沿途风景，于是商定：大部分步行上山，5名后勤改为先遣队，乘缆车上山，做好在山顶举行活动的准备，缆车速度是步行的3倍，步行同学中途在一个景点逗留了10分钟，到达山顶时比先遣队晚了半小时．

[中考真题实战]

11．为了准备小明三年后上高中的学费，他的父母准备现在拿出3000元参加教育储蓄，已知教育储蓄一年期利率为1.98%，二年期利率为2.25%，三年期利率为2.52%，请你帮小明的父母计算一下如何储蓄三年后得到的利息最多．

[开放探索创新]