
3.在式子S=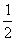 at2中,若t一定时,S与a的关系为 .
at2中,若t一定时,S与a的关系为 .
2.在 时,工作效率与工作时间成反比.
1.人的身高与体重成正比,这个说法是 的(填“正确”或“错误”).
1教学流程安排
|
活动流程图 |
活动内容和目的 |
|
活动1 检测与归纳 活动2 探究与归纳 活动3 小结与作业 |
通过对具体问题的解决,了解学生运用方程解决实际问题的水平,并归纳用方程解决实际问题的的一般方法。 通过进一步探究用一元一次方程解决综合性的实际问题,发展学生分析问题、解决问题的能力,体会建模思想。 通过师生小结,对知识归纳、整理、反思。 |
2教学过程设计
|
问题与情境 |
师生行为 |
设计意图 |
|
活动1 (一)检测方法 2008年8月8日,举世瞩目的第28届奥运会将在北京举行。现在,某商场正在热销2008年奥运会吉祥物“福娃”玩具和徽章两种奥运商品,根据图1提供的信息,求一盒“福娃”玩具和一枚徽章的价格各是多少元?    共计145元      共计280元 (二)检测技能 根据题意,列出方程(不要求解答) 1、马和驴子并肩驮着9袋包裹,驴子抱怨它驮得太多了,马回答说:“你抱怨什么?如果我从你背上拿过一包来,我的负担将是你的2倍。”问马和驴子各驮了你个包裹? 2、把一个底面半径是5㎝,高36㎝的“瘦长”圆柱锻压成底面半径20㎝的“矮胖”型圆柱,高变成了多少? 3、一队学生去校外进行军事训练,他们以每小时5千米的速度行进,走了18分钟,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以每小时14千米的速度按原路追上去,通讯员需要多少时间可以追上学生队伍? 活动2  1 2007年国庆节,小华、小颖、小明相约到“京客隆”超市调查“农夫山泉”矿泉水的日销售情况。下图是调查后三位同学进行交流的情景 1 2007年国庆节,小华、小颖、小明相约到“京客隆”超市调查“农夫山泉”矿泉水的日销售情况。下图是调查后三位同学进行交流的情景     请你根据上述对话,解答下列问题: (1) 该超市的每瓶“农夫山泉”矿泉水的标价为多少元? (2) 该超市今天销售了多少瓶“农夫山泉” 矿泉水? (温馨提示:利润=售价-进价, 利润率=  ×100%) ×100%)2某中学组织七年级学生秋游,原计划租用45座的客车若干辆,但有15人没有座位;如果租用同样数量的60座客车,则多出一辆车,且其余客车刚好坐满,已知45座客车日租金为每辆220元,60座客车日租金为每辆300元。 (1)七年级学生人数是多少?原计划租用客车多少量? (2)要使每个学生都有座位,怎样租用最省钱? 活动3 小结与作业 1你认为从实际问题中正确列出方程的关键是什么?你有哪些方法? 2你能归纳出用数学解决生活实际问题的一般过程吗? 3通过学习用一元一次方程解决实际问题,谈谈你对一元一次方程认识。 |
学生独立完成对问题1的求解过程(一位同学板演,其余同学练习本完成),并归纳用方程解决实际问题的基本步骤。 师生共同矫正。 教师重点关注: 1学生是否已经形成了用方程解决实际问题的意识。 2学生是否从图中正确分析出数量关系 3学生是否会灵活设元 4学生是否熟练的根据图表中的等量关系列出方程 5学生能否熟练解方程 6学生是否有检验的意识 学生独立完成,然后由学生代表反馈解释,全班共同矫正。 教师引导学生归纳 (1)不同类型问题中的数量关系特征,如调配问题“有得必有失”、体形变化问题中“千变万变体积不变”等。 (2)通常把哪些关系作为等量关系列方程,如可把两个量间的数量关系、把不变量的不同表达形式等作为等量关系列方程 (3)寻找等量关系的方式: 画图、列表、演示等。 学生独立思考,如果大部分学生能独立列出方程,则直接反馈矫正;反之,教师引导学生分析题中各个量之间的数量关系,寻找等量关系。 分析:(1)题中哪些量已知? 哪些量未知? (2)各个量之间有哪些数量关系? (3)由“8折”“利润率为8%”这两个条件你能得出什么? (4)对于问题1还可以根据其他的等量关系列方程吗? (5)题中的哪个量与所求“农夫山泉”矿泉水销售的瓶数有关? 教师还应结合问题1、2强调方程方法与算术方法的恰当选择。 学生独立思考,教师根据学生求解情况启发引导。 此过程中,教师重点关注: (1)学生是否能根据不同的设元方法,不同的等量关系列出不同的方程。 (2)学生是否能分析出4种租车方案,并通过计算选择出最省钱的方案。 |
通过学生独立完成对问题1的求解过程,检测学生是否形成了用方程解决实际问题的意识,以及对用方程解决实际问题的方法的掌握情况,同时提高学生信息的收集、整理和加工能力。 通过只列不解,使学生进一步熟练列方程的技能,也通过教师引导学生的归纳,使学生对寻找等量关系的方法系统化。 通过背景鲜活、贴近学生生活的实际问题的解决,提高学生分析问题、解决问题的能力,同时体会数学的应用价值。 通过用数学方法解决生活中的方案决策问题,向学生渗透数学建模思想,逐步提高学生分析问题、解决问题的能力 |
|
教 学 目 标 |
知识技能 |
能根据具体问题中的数量关系列出方程 |
|
过程方法 |
1通过对具体问题的解决,了解学生运用方程解决实际问题的水平,并归纳用方程解决实际问题的的一般方法。 2通过进一步探究用一元一次方程解决综合性的实际问题,发展学生分析问题、解决问题的能力。 |
|
|
情感态度价值观 |
通过数学方法的归纳、数学问题的解决,向学生渗透数学建模思想,体会方程是刻画现实世界的有效模型,体会数学的应用价值。 |
|
|
教学重点 |
通过实际问题的解决,提高学生对用方程解决实际问题的理解和应用水平 |
|
|
教学难点 |
用一元一次方程解决综合性的实际问题 |
|
|
教学方法 |
启发式教学法 |
|
|
教学手段 |
多媒体 |
26.(10分)某学生在做作业时,不慎将墨水瓶打翻,使一道作业题只看到如下字样:“甲、乙两地相距40千米,摩托车的速度为45千米/时,运货汽车的速度为35千米/时,(涂黑部分表示被墨水覆盖的若干文字).”请你将这道作业题补充完整,并列方程解答.
25.(10分)某地区居民生活用电基本价格为每千瓦时0.40元,若每月用电量超过a千瓦时,则超过部分按基本电价的70%收费.
(1)某户八月份用电84千瓦时,共交电费30.72元,求a.
(2)若该用户九月份的平均电费为0.36元,则九月份共用电多少千瓦时?应交电费是多少元
24.(9分)某城市为了鼓励节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10t部分,按0.45元/t收费;超过10t而不超过20t部分,按0.80元/t收费;超过20t部分,按1.5元/t收费.现已知欢欢家十月份缴水费14元,欢欢家十月份用水多少吨?
23.(9分)某天,一蔬菜经营户用70元钱从蔬菜市场批发了辣椒和蒜苗共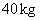 到市场去卖,辣椒和蒜苗这天的批发价与零售价如表所示:
到市场去卖,辣椒和蒜苗这天的批发价与零售价如表所示:
辣椒和蒜苗各批发了多少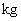 ?
?
22.(8分)某企业存入银行甲、乙两种不同性质、用途的存款共20万元,甲种存款的年利率为5.4%,乙种存款的年利率为8.28%,该企业一年可获利息收入12240元(包括利息税),问该企业存入银行的甲、乙两种存款各是多少万元?
|
品名 |
辣椒 |
蒜苗 |
批发价(单位:元/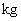 ) ) |
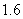 |
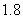 |
零售价(单位:元/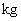 ) ) |
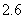 |
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com