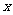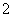1．设甲数为，乙数为，且甲数的倍与乙数的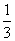的和是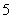，则可列方程________．

4、　　　　　　　 航行问题

对于航行问题，需注意以下几点：

(1)　　　 航行问题主要包括轮船航行和飞机航行

(2)　　　 顺水(风)速度=静水(风)速度+水流(风)速度；逆水(风)速度=静水(风)速度-水流(风)速度，顺水(风)速度-逆水(风)速度=2倍水(风)速度

(3)　　　 基本关系式：往路程=返路程

例7 有甲、乙两艘船，现同时由A地顺流而下，乙船到B地时接到通知，须立即返回C地执行任务，甲船继续顺流航行，已知甲、乙两船在静水中的速度都是每小时7.5km，水流速度为每小时2.5km，A、B两地间的距离为10km，如果乙船由A地经B地再到达C地共用了4h，问：乙船从B地到达C地时，甲船距离B地多远？

分析：本题C地可能在A、B两地之间，也可能不在A、B两地之间，所以应分两种情况分析

解：设乙船由B地航行到C地用了xh，那么甲、乙两船由A地到B地都用了(4-x)h

(1)　　　 若C地在A、B两地之间，则有(4-x)(7.5+2.5)-x(7.5-2.5)=10，解得x=2，所以甲船距离B地10×2=20(km)

(2)　　　 若C地不在A、B两地之间，则有

x(7.5-2.5)-4(4-x)(7.5+2.5)=10

解得x=，所以甲船距离B地10×=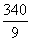(km)

答：(略)

3、　　　　　　　 环形跑道问题

一般情况下，在环形跑道上，两人同时出发，第n次相遇有两种情况：相向而行，路程和等于n圈长；同向而行，路程差等于n圈长

例6　　　　　 小王每天去体育场晨练，每次都见到一位田径队的叔叔也在锻炼，两人沿400米跑道跑步，每次总是小王跑2圈的时间叔叔跑3圈，一天，两人在同地反向而跑，小明看了一下记时表，发现隔了32秒两人第一次相遇，求两人的速度；第二天小王打算和叔叔在同地同向而跑，看叔叔隔多少时间首次与他相遇，你能先帮小王预测一下吗？

例7　　　　　 分析：第一问依路程和列方程，第二问以路程差列方程

解：设叔叔的速度为3Vm/s，则小王的速度为2Vm/s

根据题意，得(3V+2V)32=400，解得V=2.5

∴3V=3×2.5=7.5m/s　 2V=2×2.5=5m/s

即叔叔的速度为7.5m/s，小王的速度为5m/s

第二天同地同向跑时，设xs首次相遇

依题意，得7.5x-5x=400，解得x=160，即160s后首次相遇

点评：本题隐含一个条件是小王与叔叔的速度比为2：3

2、　　　　　　　 追及问题

(1)　　　 同地追及。基本关系式：快者路程=慢者路程

例4　　　　　 一队学生在校外进行军事野营训练，他们以5km/h的速度行进，走了18min的时候，学校要将一个紧急通知传给队长，通讯员从学校出发，骑自行车以14km/h的速度按原路追去，问通讯员用多少时间可以追上学生队伍？

分析：本题以一队学生所走路程=通讯员骑车路程列方程

解：设通讯员用xh可以追上学生队伍，依题意，得

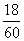5(x+)=14x

解这个方程，得x=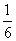

答：(略)

(2)　　　 异地追及：基本关系式：快者路程-慢者路程=两地距离

例5　 A、B两站间的距离为448km，一列慢车从A站出发，每小时行驶60km，一列快车从B站出发，每小时行驶80km，问经过几小时快车能追上慢车？

分析：本题虽未明确两车的行驶方向，但既然快车能追上慢车，则两车只能沿从A到B的方向同向而行

解：设经过xh快车能追上慢车，根据题意得 80x-60x=448，解得x=22.4，答：(略)

行程问题，它涉及路程、速度和时间三个基本量，在匀速条件下，它们的基本关系是：路程=速度×时间，行程问题又分为以下四种情况

1、　　　　　　　 相遇问题

基本关系式：快者路程+慢者路程=两地距离

例3　 甲、乙两列火车从A、B两地相向而行，乙车比甲车早发车1h，甲车比乙车速度每小时快30km，甲车发车两小时恰好与乙车相遇，相遇后为了错车，甲车放慢了速度，以它原来的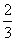速度行驶；而乙车加快了速度，以它原来的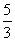倍飞速行驶，结果2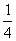h后，两车距离又等于A、B两地之间的距离，求两车相遇前速度及A、B两地之间的距离。

分析：本题以甲乙相遇时，距离=相遇后经过2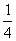h后甲、乙间距离列方程

解析：设相遇前乙车的速度为xkm/h，则相遇前、后两车行驶的路程可由图1表示出来

依题意得3x+2(x+30)=[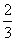(x+30)+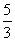x]×，解得x=60

则x+30=90(km/h)，3x+2(x+30)=3×60+2×90=360(km)

答：(略)

工程问题经常把总工作量看成1，存在等量关系：工作效率×工作时间=工作量，工作量的和=1

例1　 某单位开展植树活动，由一人植树要80小时完成，现由一部分人先植树5小时，由于单位有紧急事情，再增加2人，且必须在4小时之内完成植树任务，这些人的工作效率相同，应先安排多少人植树？

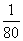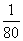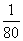分析：把工作量看作1，每一个人的工作效率为，由x人先做5小时，完成的工作量为×5×x=x，增加2人后，4小时完成的工作量为×(x+2)×4=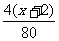，由5小时的工作量×4小时的工作量=工作总量，可列方程

解：设安排x人先工作5小时，根据工作总量等于各分量之和，得+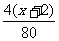=1

解得x=8，答：(略)

例2　 某车间接到一批加工任务，计划每天加工120件，可以如期完成，实际加工时每天多加工20件，结果提前4天完成任务，问这批加工任务共有多少件？

分析：假设这批加工任务一共有x件，那么计划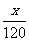天完成，而实际用了天完成，所以由等量关系：计划用的时间 -实际用的时间=4，列方程

解：设这批加工任务共有x件，依题意得

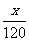-=4

解得x=3360，答：(略)

例5　 某所中学现有学生4200人，计划一年后初中在校生增加8%，高中在校生增加11%，这样全校在校生将增加10%，问：这所学校现在的初中在校生和高中在校生人数分别是多少？

分析：本题等量关系是：一年后初中在校生增加的人数+高中在校生增加的人数=全校在校生增加的总人数

解：设这所学校现在的初中在校生人数为x人，则现在的高中在校生为(4200-x)人，由题意可得8%·x+(4200-x)×11%=4200×10%，解得x=1400

当x=1400时，4200-x=2800

答：这所学校现在的初中在校生人数为1400人，现在的高中在校生人数为2800人。

解决这类问题关键在于如何巧妙设出未知数，从而化简计算，常用的设未知数方法是：①连续数设中间；②多位自然数设一位；③数字换位设部分；④小数点移动直接设；⑤数字成比例设比值；⑥特殊关系特殊设

例4　　　　　 一个四位整数，其个位数字为2，若把末位数字移到首位，所得新数比原数小108，求这个四位数。

分析：本题依新数减去原数等于108列方程。

解：设这个四位数的前三位数为x，由此四位数为10x+2，末位数移到首位后所得新数为1000×2+x，则

(10x+2)-(1000×2+x)=108

解得x=234

所以10x+2=2343

答：所求四位数为2342。

(1)　　　 商品利润=商品售价-商品进价(即商品成本)

(2)　　　 商品利润率=×100%

(3)　　　 折扣率：打n折，指按售价为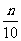售出，n折可以是小数(如8.5折)

例3　 某商品的进价是1530元，按商品标价的9折出售时，利润率是15% ，商品的标价是多少元？

分析：本题由利润=进价×利润率=标价×折扣率-进价列方程

解：设此商品的标价是x元，则

0.9x-1530=1530×15%　　

解得x=1955

答：此商品的标价是1955。

元。

本类问题依调动后列等量关系　　　　　　　　　　　　　　　　　　　

例2　　　　　　　　 甲、乙两个工程队分别有80人和60人，为了支援乙队，需要从甲队调出一部分人进乙队，使乙队的人数比甲队人数的2倍多5人，问从甲队调出的人数应是多少？

分析：本题以调动后，乙队比甲队的人数的2倍多5人列方程

解：应从甲队调出人进乙队，则调动后的等量关系是：乙队的人数=甲队的人数×2+5，所以60+x=2(80-x)+5　 解之得x=35

答：从甲队调出的人是35。