
5.菱形对角线的交点为O,以O为圆心,以O到菱形一边的距离为半径的圆与其他几边的关系为( )
A.相交 B.相切 C.相离 D.不能确定
4.以三角形的一边长为直径的圆切三角形的另一边,则该三角形为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
3.⊙O内最长弦长为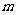 ,直线
,直线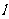 与⊙O相离,设点O到
与⊙O相离,设点O到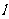 的距离为
的距离为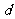 ,则
,则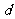 与
与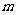 的关系是( )
的关系是( )
A.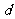 =
=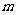 B.
B.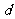 >
>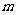 C.
C.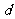 >
>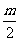 D.
D.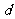 <
<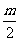
2.Rt△ABC中,∠C=90°,AB=10,AC=6,以C为圆心作⊙C和AB相切,则⊙C的半径长为( )
A.8 B.4 C.9.6 D.4.8
1.若∠OAB=30°,OA=10cm,则以O为圆心,6cm为半径的圆与射线AB的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
 如图3-29,C是⊙O的直径AB延长线上一点,D是⊙O上一点,∠A =
27°,∠C = 36°,试判断直线CD与⊙O的位置关系,并证明你的结论.
如图3-29,C是⊙O的直径AB延长线上一点,D是⊙O上一点,∠A =
27°,∠C = 36°,试判断直线CD与⊙O的位置关系,并证明你的结论.
[综合练习]
 已知:如图3-30,BC是⊙O的直径,A是弦BD延长线上一点,切线DE交AC于点E,且AE = EC.
你能确定AC与⊙O的位置关系吗?请说明理由.
已知:如图3-30,BC是⊙O的直径,A是弦BD延长线上一点,切线DE交AC于点E,且AE = EC.
你能确定AC与⊙O的位置关系吗?请说明理由.
[探究练习]
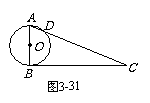 如图3-31,已知:在Rt△ABC中,∠B = 90°,AC = 13 cm,AB = 5 cm,O是AB上的一点,以O为圆心,OB为半径作⊙O.
如图3-31,已知:在Rt△ABC中,∠B = 90°,AC = 13 cm,AB = 5 cm,O是AB上的一点,以O为圆心,OB为半径作⊙O.
(1)当OB = 2.5 cm时,⊙O交AC于点D,
试求CD的长;
(2)当OB = 2.4 cm时,AC与⊙O有怎样的位置关系?并证明你的结论.
练习二
[基础练习]一、1. 相切; 2. 相切; 3. 6.5 cm,2 cm. 二、1. D; 2. B. 三、CD与⊙O相切(提示:连接OD,证∠ODC = 90°.
[综合练习]提示:证BC⊥AC.
[探究练习](1);(2)AC与⊙O相切(提示:过O作OE⊥AC,设垂足为E,证OE = 2.4 cm).
2. 在△ABC中,∠C = 90°,AC = 12 cm,BC = 16 cm,O是AB边上的一点,以O为圆心的⊙O与AC、BC都相切,则⊙O的直径长为( ).
A. 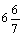 cm B.
cm B. 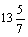 cm C. 4 cm D.
cm C. 4 cm D.  cm
cm
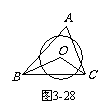
1. 如图3-28,△ABC中,∠A = 70°,⊙O在△ABC的三条边上所截得的弦长都相等,则∠BOC的度数是( );
A. 140° B. 135°
C. 130° D. 125°
3. 在△ABC中,∠C =
90°,AC = 12 cm,BC = 5 cm,则它的外接圆半径R = cm,内切圆半径r = cm.
在△ABC中,∠C =
90°,AC = 12 cm,BC = 5 cm,则它的外接圆半径R = cm,内切圆半径r = cm.
2. 已知:如图3-27,AB是⊙O的弦,C是半径OA延长线上一点,若AC = OA = AB,则BC与⊙O的位置关系是 ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com