
2.探索直线与圆的三种位置关系
(1)从公共点个数来判断
(2)从点到直线的距离d与半径r间的数量关系来判断.
备课资料
参考例题
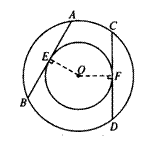 如下图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E.
如下图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E.
求证:CD与小圆相切.
分析:因为已知条件没
给出CD与小圆有公共点,所
以可过圆心O作OF⊥CD,设
垂足为F,只要证明OF等于
小圆的半径即可.因为AB和
小圆相切于E,连接OE,可知OE⊥AB,又AB、CD为大圆的弦,而且相等,而OE=OF分别为两弦的弦心距,因此有OE、OF,得证.
证明:连接OE,过O作OF⊥CD,垂足为F,
∵AB与小圆O切于点E,
∴OE⊥AB.
又∵OF⊥CD,AB=CD,
∴OF=OE.
∵OF⊥CD,∴CD与小圆O相切.
4.例题讲解
3.如何作三角形的内切圆
2.做一做
备课资料
参考例题
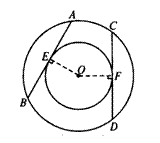 如下图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E.
如下图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E.
求证:CD与小圆相切.
分析:因为已知条件没
给出CD与小圆有公共点,所
以可过圆心O作OF⊥CD,设
垂足为F,只要证明OF等于
小圆的半径即可.因为AB和
小圆相切于E,连接OE,可知OE⊥AB,又AB、CD为大圆的弦,而且相等,而OE=OF分别为两弦的弦心距,因此有OE、OF,得证.
证明:连接OE,过O作OF⊥CD,垂足为F,
∵AB与小圆O切于点E,
∴OE⊥AB.
又∵OF⊥CD,AB=CD,
∴OF=OE.
∵OF⊥CD,∴CD与小圆O相切.
4.例题讲解
3.如何作三角形的内切圆
2.做一做
备课资料
参考练习
填写下表
直线与圆的三种位置关系
|
直线和圆的位置 |
相交 |
相切 |
相离 |
|
公共点个数 |
|
|
|
|
圆心到直线的距离d与半径r的关系 |
|
|
|
|
公共点名称 |
|
|
|
|
直线名称 |
|
|
|
答案:2 1 0 d<r d<r d>r 交点 切点 无 剖线 切线 无
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com