
3.例题教学
例2是梯形中位线的性质的应用.
这是一个计算问题,解答中比较多地用到了代数运算。
2.探索活动
活动一 操作--观察--探索.
课本中的操作活动是对“情境创设”中提出的问题的解读.
活动分为3个层次.
第一层次:操作、观察--按课本要求,将△ADN绕点N旋转180°,得△ABE。
教学中,应使学生理解:这一操作活动的实质是构造两个关于点N成中心对称的△ADN和△ENC从而为利用中心对称性质研究梯形中位线的性质做铺垫.
第二层次:探索MN与BE之间的关系?并说明理由.
这一层次既是对将要探究的梯形中位线性质的一个铺垫,又渗透了转化的思想方法--将对梯形中位线性质的研究转化为对三角形中位线性质的研究.
第三层次:引入梯形中位线的概念.
对梯形中位线的概念,要强调它是连接梯形的两腰中点的线段,而不是连接梯形的两底中点的线段.
活动二 探索梯形中位线的性质.
教学中,要引导学生在“活动一”的基础上,通过独立思考和合作交流,得出梯形中位线的性质:由△ADN≌△ECN,得AN=NE,MN是△ABE的中位线,所以MN∥BC,MN=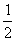 BE.又AD∥BC,AD=CE,所以:AD∥MN∥BC,MN=
BE.又AD∥BC,AD=CE,所以:AD∥MN∥BC,MN=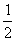 (AD+BC).
(AD+BC).
梯形中位线的性质是梯形的一个重要性质,同三角形中位线的性质一样,教学中,应引导学生归纳这个性质的特点:在同一条件下,有2个结论,一个表示位置关系,另一个表示数量关系.因此,应用该性质时,要注意根据需要,选用结论.
值得注意的是:从梯形中位线的公式MN=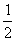 (AD+BC)可以看出,当AD变为一点,即AD的长度为0时,公式变为MN=
(AD+BC)可以看出,当AD变为一点,即AD的长度为0时,公式变为MN=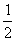 (0+BC),成为三角形中位线的公式,这反映了2个性质的内在联系,即三角形中位线的性质是梯形中位线性质的特例.
(0+BC),成为三角形中位线的公式,这反映了2个性质的内在联系,即三角形中位线的性质是梯形中位线性质的特例.
1.情境创设
怎样将一张梯形硬纸片剪成两部分,使分成的两部分能拼成一个三角形?
3.经历探索三角形中位线、梯形中位线性质的过程,体会转化的思想方法.
[教学过程(第二课时)l
2.会利用三角形中位线、梯形中位线的性质解决有关问题.
1.探索并掌握三角形中位线、梯形中位线的概念、性质.
3.6三角形、梯形的中位线
[教学目标]
4.小结
(1)学习了三角形中位线的性质;
(2)利用三角形中位线的概念和性质解决有关问题;
(3)经历了探索三角形中位线性质的过程,体会转化的思想方法.
3.例题教学
例1是三角形中位线的性质的应用。
教学中,可先让学生画一个任意四边形,再顺次连接四边形各边的中点,然后猜想探索得到的四边形的形状,并说明理由.
解答中,由EF∥AC,HG∥AC,得EF∥HG。理由是:如果两条直线都与第三条直线平行,那么这两条直线互相平行.
例1得到的结论是:顺次连接四边形各边中点的线段组成一个平行四边形.教学中,在此基础上,可提出下列问题组织学生思考、交流:
(1)顺次连接矩形4边中点所得的四边形是怎样的图形?为什么?
(2)如果将矩形改成菱形,结果怎样?
2.探索活动活动一 操作--观察--探索.
课本中的操作活动是对“情境创设”中提出的问题的解读.
活动分为3个层次.
第一层次:操作、观察--按课本要求,将△ADE绕点E旋转180°,得四边形BCFD.
教学中,应使学生理解:这一操作活动的实质是构造两个关于点O成中心对称的△ADE与△CEF,从而为下面利用中心对称性质研究三角形中位线的性质做铺垫.
第二层次:判别四边形BCFD是否是平行四边形?并说明理由.
这一层次既是对将要探究的三角形中位线性质的一个铺垫,又渗透了转化的思想方法--将对三角形中位线性质的研究转化为对平行四边形性质的研究.
第三层次:引入三角形中位线的概念.
对三角形的中线与三角形的中位线的概念学生容易混淆,教学中,应要求学生画出相应的图形,说出它们之间的区别.
活动二 探索三角形中位线的性质。
教学中,要引导学生在“活动一”的基础上,通过独立思考和合作交流,得出三角形中位线的性质:由△AD0≌△CFE,得EF=DE=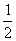 DF。又由四边形BCFD是平行四边形,得DE∥BC,DE=
DF。又由四边形BCFD是平行四边形,得DE∥BC,DE=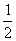 DF=
DF=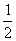 BC.
BC.
三角形中位线的性质是三角形的一个重要性质,教学中,应引导学生归纳这个性质的特点:在同一条件下,有2个结论,一个表示位置关系,另一个表示数量关系,因此,应用该性质时,要注意根据需要,选用结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com