1、画一画，观察与思考：画△ABC的中线BE，取边AB上的中点D，连接DE，线段DE是中线吗？

怎样将一张三角形纸片剪成两部分，使分成的两部分能拼成一个平行四边形？

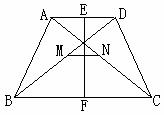
4、已知：如图，在梯形ABCD中，AD∥BC，AB=DC，E、F、M、N分别是AD、BC、BD、AC的中点。试说明：EF与MN互相垂直平分。

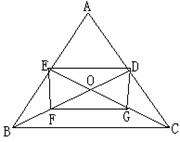
3、已知：如图矩形ABCD的对角线相交于点O，E、F分别是OA、OD的中点。

试说明：四边形CBEF是等腰梯形。

2、已知：如图，在△ABC中，中线BD、CE相交于点O，F、G分别是OB、OC的中点。

试说明：四边形DEFG是平行四边形。

1、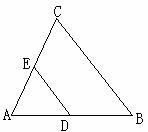已知：如图，在△ABC中，D是AB的中点，DE∥BC交AC于点E。

试说明：DE=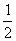BC。

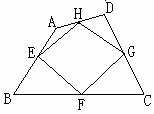例1：如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、、DA的中点。四边形EFGH是平行四边形吗？为什么？

例2：如图，矩形ABCD的对角线相交于点O，点E、F、G、H分别是OA、OB、OC、DO的中点，四边形EFGH是矩形吗？为什么？

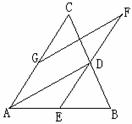例3：已知：如图，AD是△ABC的中线，E、G分别是AB、AC的中点，GF∥AD交ED的延长线于点F。

⑴猜想：EF与AC有怎样的关系？

⑵试证明你的猜想。

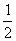例4：已知在△ABC中，∠B=2∠C，AD⊥BC于D，M为BC的中点。试说明DM=AB

例5：等腰梯形ABCD中，AD∥BC，EF为中位线，EF=18，AC⊥AB，∠B=60°，求梯形ABCD的周长及面积。

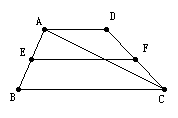
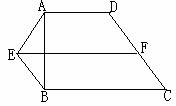例6、已知：如图，在梯形ABCD中，AD∥BC，∠ABC=90°，E是梯形外一点，且AE=BE，F是CD的中点。试说明：EF∥BC。

例7：如图，在梯形ABCD中，AD∥BC，M、N分别是两条对角线BD、AC的中点，试说明：MN∥BC且MN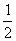＝(BC－AD)。

例8：已知：如图，四边形ABCD为等腰梯形，AD∥BC，AC、BD相交于点O，点P、Q、R分别为AO、BO、CD的中点，且∠AOD＝60°。试判断ΔPQR的形状，并说明理由？

2、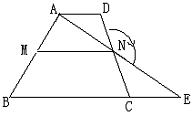梯形的中位线：

⑴连结梯形两腰中点的线段叫做梯形的中位线。

注意：中位线是两腰中点的连线，而不是两底中点的连线。

⑵梯形中位线的性质

梯形的中位线平行于两底，并且等于两底和的一半。

1、三角形的中位线：

⑴连结三角形两边中点的线段叫做三角形的中位线．

区别三角形的中位线与三角形的中线。

⑵三角形中位线的性质

三角形的中位线平行于第三边并且等于它的一半．

4．小结

　　 (1)学习了梯形中位线的性质；

　　 (2)利用梯形中位线的概念和性质解决有关问题；

(3)经历了探索梯形中位线性质的过程，体会转化的思想方法．