2．如果两个圆相切，那么切点和两圆的圆心_____．

备课资料

　　 参考练习

1．⊙O₁和⊙O₂的半径分别为3 cm和4cm，若两圆外切，则d＝_____；若两圆内切；则d＝____．

5．议一议

4．想一想

3．例题讲解

2．探索圆和圆的位置-关系

3．探讨在两圆外切或内切时，圆心距d与R和r之间的关系．

　　 Ⅴ．课后作业

　　 习题3．9

　　 Ⅵ．活动与探究

已知图中各圆两两相切，⊙O的半径为2R，⊙O₁、⊙O₂的半径为R，求⊙O₃的半径．

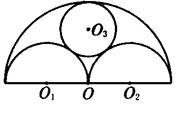
　　 分析：根据两圆相外切连心线的长为两半径之和，如果设⊙O₃的半径为r，则O₁O₃=O₂O₃＝R+r，连接OO₃就有OO₃⊙O₁O₂，所以OO₂O₃构成了直角三角形，利用勾股定理可求得⊙O₃的半径r.

　　 解：连接O₂O₃、OO₃，

　　 ∴O₂OO₃＝90°，OO₃＝2R-r

　　 O₂O₃＝R+r，OO₂＝R

　　 ∴(R+r)²=(2R-r)²+R²．

　　 ∴r=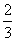R

板书设计

§3．6　 圆和圆的位置关系

2．讨论在两圆外切或内切情况下，图形的轴对称性及对称轴，以及切点和对称轴的位置关系；

　　 投影片(§ 3．6 C)

设两圆的半径分别为R和r．

(1)当两圆外切时，两圆圆心之间的距离(简称圆心距)d与R和r具有怎样的关系?反之当d与R和r满足这一关系时，这两个圆一定外切吗?

(2)当两圆内切时(R>r)，圆心距d与R和r具有怎样的关系?反之，当d与R和r满足这一关系时，这两个圆一定内切吗?

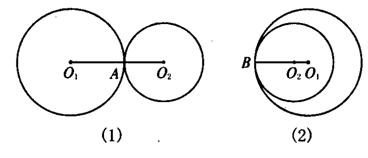
　　 [师]如图，请大家互相交流．

　　 [生]在图(1)中，两圆相外切，切点是A．因为切点A在连心线O₁O₂上，所以O₁O₂＝O₁A+O₂A＝R+r，即d=R+r：反之，当d＝R+r时，说明圆心距等于两圆半径之和，O₁、A、O₂在一条直线上，所以⊙O₁与⊙O₂只有一个交点A，即⊙O₁与⊙O₂外切．

　　 在图(2)中，⊙O₁与⊙O₂相内切，切点是B.因为切点B在连心线O₁O₂，所以O₁O₂＝O₁B-O₂B，即d＝R-r：反之，当d＝R-r时，圆心距等于两半径之差，即O₁O₂=O₁B-O₂B，说明O₁、O₂、B在一条直线上，B既在⊙O₁上，又在⊙O₂上，所以⊙O₁与⊙O₂内切．

　　 [师]由此可知，当两圆相外切时，有d=R+r，反过来，当d=R+r时，两圆相外切，即两圆相外切d＝R+r

　　 当两圆相内切时，有d=R-r，反过来，当d＝R-r时，两圆相内切，即两圆相内切d＝R-r．

　　 Ⅲ．课堂练习

　　 随堂练习

　　 Ⅳ．课时小结

　　 本节课学习了如下内容：

1．探索圆和圆的五种位置关系；

如图(1)，⊙O₁与⊙O₂外切，这个图是轴对称图形吗?如果是，它的对称轴是什么?切点与对称轴有什么位置关系?如果⊙O₁与⊙O₂内切呢?[如图(2)]

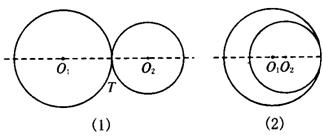
　　 [师]我们知道圆是轴对称图形，对称轴是任一直径所在的直线，两个圆是否也组成一个轴对称图形呢?这就要看切点了是否在连接两个圆心的直线上，下面我们用反证法来证明．反证法的步骤有三步：第一步是假设结论不成立；第二步是根据假设推出和已知条件或定理相矛盾的结论；第三步是证明假设错误，则原来的结论成立．

　　 证明：假设切点丁不在O₁O₂上．

　　 因为圆是轴对称图形．所以T关于O₁O₂的对称点广也是两圆的公共点，这与已知条件⊙O₁和⊙O₂相切矛盾，因此假没不成立．

　　 则T在O₁O₂上．

　　 由此可知图(1)是轴对称图形，对称轴是两圆的连心线，切点与对称轴的位置关系是切点在对称轴上．

　　 在图(2)中应有同样的结论．

　　 通过上面的讨论，我们可以得出结论：两圆相内切或外切时，两圆的连心线一定经过切点，图(1)和图(2)都是轴对称图形，对称轴是它们的连心线．