4．两圆半径之比为3：5，当两圆内切时，圆心距为4 cm，则两圆外切时圆心距的长为_____．

3．半径为5 cm的⊙O外一点P，则以点P为圆心且与⊙O相切的⊙P能画_______个．

2．如果两个圆相切，那么切点和两圆的圆心_____．

备课资料

　　 参考练习

1．⊙O₁和⊙O₂的半径分别为3 cm和4cm，若两圆外切，则d＝_____；若两圆内切；则d＝____．

5．议一议

4．想一想

3．例题讲解

2．探索圆和圆的位置-关系

3．探讨在两圆外切或内切时，圆心距d与R和r之间的关系．

　　 Ⅴ．课后作业

　　 习题3．9

　　 Ⅵ．活动与探究

已知图中各圆两两相切，⊙O的半径为2R，⊙O₁、⊙O₂的半径为R，求⊙O₃的半径．

　　 分析：根据两圆相外切连心线的长为两半径之和，如果设⊙O₃的半径为r，则O₁O₃=O₂O₃＝R+r，连接OO₃就有OO₃⊙O₁O₂，所以OO₂O₃构成了直角三角形，利用勾股定理可求得⊙O₃的半径r.

　　 解：连接O₂O₃、OO₃，

　　 ∴O₂OO₃＝90°，OO₃＝2R-r

　　 O₂O₃＝R+r，OO₂＝R

　　 ∴(R+r)²=(2R-r)²+R²．

　　 ∴r=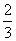R

板书设计

§3．6　 圆和圆的位置关系

2．讨论在两圆外切或内切情况下，图形的轴对称性及对称轴，以及切点和对称轴的位置关系；