3．圆的圆心角是多少度?

　　 [生]若圆的半径为r，则周长l＝2πr，面积S＝πr²，圆的圆心角是360°．

1．圆的周长如何汁算?

　　 2，圆的面积如何计算?

6．扇形面积的应用．

5．弧长及扇形面积的关系；

4．想一想；

3．例题讲解；

2．探索弧长的计算公式；

3．探索弧长l及扇形的面积S之间的关系，并能已知一方求另一方．

Ⅴ．课后作业

习题3．10

Ⅵ．活动与探究

如图，两个同心圆被两条半径截得的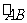的长为6π cm，的长为10π cm，又AC＝12cm，求阴影部分ABDC的面积．

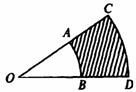
分析：要求阴影部分的面积，需求扇形COD的面积与扇形AOB的面积之差．根据扇形面积S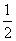＝lR，l已知，则需要求两个半径OC与OA，因为OC＝OA+AC，AC已知，所以只要能求出OA即可．

解：设OA＝R，OC＝R+12，∠O＝n°，根据已知条件有：

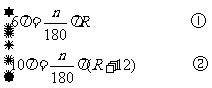
得．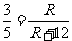

∴3(R+12)＝5R，∴R＝18．

∴OC＝18+12＝30．

∴S＝S_扇形COD－S_扇形AOB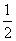＝×10π×30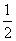－×6π×18＝96π cm²．

所以阴影部分的面积为96π cm²．

板书设计

§3．7　 弧长及扇形的面积

2．探索扇形的面积公式S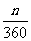＝πR²，并运用公式进行计算；

投影片(§3．7D)

扇形AOB的半径为12cm，∠AOB＝120°，求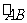的长(结果精确到0.1cm)和扇形AOB的面积(结果精确到0.1cm²)

分析：要求弧长和扇形面积，根据公式需要知道半径R和圆心角n即可，本题中这些条件已经告诉了，因此这个问题就解决了．

解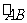：的长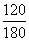＝π×12≈25.1cm．

S_扇形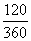＝π×12²≈150.7cm²．

因此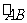，的长约为25.1cm，扇形AOB的面积约为150.7cm²．

Ⅲ．课堂练习

随堂练习

Ⅳ．课时小结

本节课学习了如下内容：

1．探索弧长的计算公式l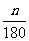＝πR，并运用公式进行计算；