投影片(§ 3．7 A)

　如图，某传送带的一个转动轮的半径为10cm

．

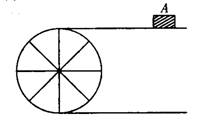
　 (1)转动轮转一周，传送带上的物品A被传送多少厘米?

　 (2)转动轮转1°，传送带上的物品A被传送多少厘米?

　 (3)转动轮转n°，传送带上的物品A被传送多少厘米?

　　 [师]分析：转动轮转一周，传送带上的物品应被传送一个圆的周长；因为圆的周长对应360°的圆心角，所以转动轮转1°，传送带上的物品A被传送圆周长的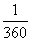；转动轮转n°，传送带上的物品A被传送转l°时传送距离的n倍．

　　 [生]解：(1)转动轮转一周．传送带上的物品A被传送2π×10＝20πcm；

　　 (2)转动轮转1°，传送带上的物品A被传送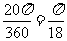cm；

　　 (3)转动轮转n°，传送带上的物品A被传送n×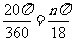cm．

　　 [师]根据上面的计算，你能猜想出在半径为R的圆中，n°的圆心角所对的弧长的计算公式吗?请大家互相交流．

　　 [生]根据刚才的讨论可知，360°的圆心角对应圆周长2πR，那么1°的圆心角对应的弧长为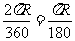，n°的圆心角对应的弧长应为1°的圆心角对应的弧长的n倍，即n×.

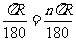　　 [师]表述得非常棒．

在半径为R的圆中，n°的圆心角所对的弧长(arclength)的计算公式为：

　l=.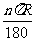

　　 下面我们看弧长公式的运用．

3．圆的圆心角是多少度?

　　 [生]若圆的半径为r，则周长l＝2πr，面积S＝πr²，圆的圆心角是360°．

1．圆的周长如何汁算?

　　 2，圆的面积如何计算?

　　 如图，两个同心圆被两条半径截得的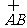的长为6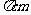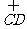，的长为10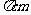，又AC=12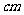，求阴影部分ABDC的面积．

　　 分析：要求阴影部分的面积，需求扇形COD的面积与扇形AOB的面积之差．根据扇形面积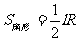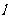，已知，则需要求两个半径0C与OA，因为OC＝OA+AC，AC已知，所以只要能求出OA即可．

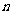　　 解：设OA=R，0C＝R十12，∠O＝°，根据已知条件有：

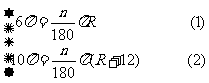
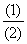得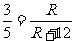

∴3(R+12)=5R

∴R=18

∴OC=18+12=30

∴S=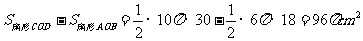

　　 所以阴影部分的面积为96．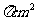

2．课本P142习题　 1、2、3

1．复习本课的内容；

3．探索弧长及扇形的面积之间的关系，并能已知一方求另一方。

2．探索扇形的面积公式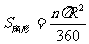，并运用公式进行计算；

　　 本节课学习了如下内容：

1．探索弧长的计算公式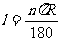，并运用公式进行计算；

4．随堂练习:课本P141　 1、2