投影片(§3．8 A)

　 圣诞节将近，某家商店正在制作圣诞节的圆锥形纸帽．已知纸帽的底面周长为58 cm，高为20cm，要制作20顶这样的纸帽至少要用多少平方厘米的纸?(结果精确到0．1cm²)

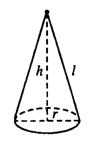　　 分析：根据题意，要求纸帽的面积，

即求圆锥的侧面积．现在已知底面圆的

周长，从中可求出底面圆的半径，从而

可求出扇形的弧长，在高h、底面圆的半

径r、母线l组成的直角三角形中，根据勾

股定理求出母线l，代入S_侧=πrl中即可．

　　 解：设纸帽的底面半径为r cm，母线长为lcm，则r=,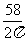

　　 l=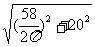≈22．03cm，

　　 S_圆锥侧=πrl≈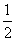×58×22．03=638．87cm²．

638．87×20＝12777．4 cm²．

　　 所以，至少需要12777．4 cm²的纸．

　 投影片(§3．8 B)

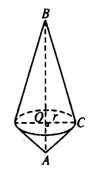
　 如图，已知Rt△ABC

的斜边AB＝13cm，一条

直角边AC=5 cm，以直线

AB为轴旋转一周得一个几

何体．求这个几何体的表

面积．

　　 分析：首先应了解这个几何体

的形状是上下两个圆锥，共用一个底面，表面积即为两个圆锥的侧面积之和．根据S_侧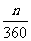＝πR²或S_侧=πrl可知，用第二个公式比较好求，但是得求出底面圆的半径，因为AB垂直于底面圆，在Rt△ABC中，由OC、AB=BC、AC可求出r，问题就解决了．

　　 解：在Rt△ABC中，AB＝13cm,AC＝5cm，

　　 ∴BC=12 cm．

　　 ∵OC·AB＝BC·AC，

　　 ∴r=OC=．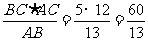

　　 ∴S_表=πr(BC+AC)= π×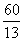×(12+5)

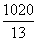　　 =πcm²．

　　 Ⅲ．课堂练习

　　 随堂练习

　　 Ⅳ．课时小结

　　 本节课学习了如下内容：

　　 探索圆锥的侧面展开图的形状，以及面积公式，并能用公式进行计算．

　　 Ⅴ．课后作业

　　 习题3．11

　　 Ⅵ．活动与探究

　　 探索圆柱的侧面展开图

　　 在生活中，我们常常遇到圆柱形的物体，如油桶、铅笔、圆形柱子等，在小学我们已知圆柱是由两个圆的底面和一个侧面围成的，底面是两个等圆，侧面是一个曲面，两个底面之间的距离是圆柱的高．

　　 圆柱也可以看作是由一个矩形旋转得到的，旋转轴叫做圆柱的轴，圆柱侧面上平行于轴的线段都叫做圆柱的母线．容易看出，圆柱的轴通过上、下底面的圆心，圆柱的母线长都相等，并等于圆柱的高，圆柱的两个底面是平行的．

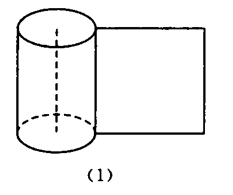　　 如图，把圆柱的侧

面沿它的一条母线剪开，

展在一个平面上，侧面

的展开图是矩形，这个

矩形的一边长等于圆柱

的高，即圆柱的母线长，

另一边长是底面圆的周长，

所以圆柱的侧面积等于底

面圆的周长乘以圆柱的高．

[例1]如图(1)，把一个圆柱形木块沿它的轴剖开，得矩形ABCD．已知AD=18 cm，AB＝30 cm，求这个圆柱形木块的表面积(精确到1 cm²)．

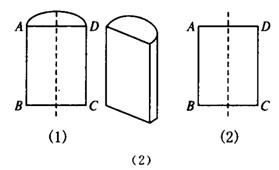
　　 解：如图(2)，AD是圆柱底面的直径，AB是圆柱的母线，设圆柱的表面积为S，则S=2S_圆+S_侧．

　　 ∴S=2π(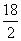)²+2π×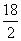×30=162π+540π≈2204 cm²．

　　 所以这个圆柱形木块的表面积约为2204 cm²

板书设计

§3．8　 圆锥的侧面积

　　 [师](向学生展示圆锥模型)请大家先观察模型，再展开想象，讨论圆锥的侧面展开图是什么形状．

　　 [生]圆锥的侧面展开图是扇形．

　　 [师]能说说理由吗?

　　 [生甲]因为数学知识是一环扣一环的，后面的知识是在前面知识的基础上学习的．上节课的内容是弧长及扇形面积，本节课的内容是圆锥的侧面积，而弧长不是面积，所以我猜想圆锥的侧面展开图应该是扇形．

　　 [师]这位同学用的虽然是猜想，但也是有一定的道理的，并不是凭空瞎想，还有其他理由吗?

　　 [生乙]我是自己实践得出结论的，我拿一个扇形的纸片卷起来，就得到了一个圆锥模型．

　　 [师]很好，究竟大家的猜想是否正确呢?下面我就给大家做个演示(把圆锥沿一母线剪开)，请大家观察侧面展开图是什么形状的?

　　 [生]是扇形．

　　 [师]大家的猜想非常正确，既然已经知道侧面展开图是扇形，那么根据上节课的扇形面积公式就能计算出圆锥的侧面积，由于我们不能把所有圆锥都剖开，在展开图中的扇形的半径和圆心角与不展开图形中的哪些因素有关呢?这将是我们进一步研究的对象．

　　 二、探索圆锥的侧面积公式

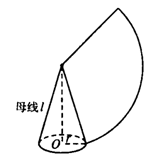
　　 [师]圆锥的侧面展开图是

一个扇形，如图，设圆锥的母

线(generating line)长为l，

底面圆的半径为r，那么这个圆

锥的侧面展开图中扇形的半径即

为母线长l，扇形的弧长即为底

面圆的周长2πr，根据扇形面积公式

可知S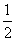＝·2πr·l＝πrl．因此圆锥的侧面积为S_侧＝πrl．

　　 圆锥的侧面积与底面积之和称为圆锥的全　 面积(surfacearea)，全面积为S_全=πr²+πrl．

3．利用圆锥的侧面积公式进行计算．

2．探索圆锥的侧面积公式；

投影片(§3．8A)

圣诞节将近，某家商店正在制作圣诞节的圆锥形纸帽．已知纸帽的底面周长为58cm，高为20cm，要制作20顶这样的纸帽至少要用多少平方厘米的纸？(结果精确到0.1cm)²

分析：根据题意，要求纸帽的面积，即求圆锥的侧面积．现在已知底面圆的周长，从中可求出底面圆的半径，从而可求出扇形的弧长．在高h、底面圆的半径r、母线l组成的直角三角形中，根据勾股定理求出母线l，代入S_侧＝πrl中即可．

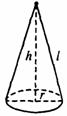
解：设纸帽的底面半径为r cm，母线长为l cm，则r＝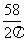

l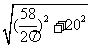＝≈22.03cm，

S_圆锥侧＝πrl≈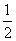×58×22.03＝638.87cm²．

638.87×20＝12777.4cm²．

所以，至少需要12777.4cm²的纸．

投影片(§3．8B)

如图，已知Rt△ABC的斜边AB＝13cm，一条直角边AC＝5cm，以直线AB为轴旋转一周得一个几何体．求这个几何体的表面积．

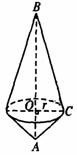
分析：首先应了解这个几何体的形状是上下两个圆锥，共用一个底面，表面积即为两个圆锥的侧面积之和．根据S_侧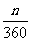＝πR²或S_侧＝πrl可知，用第二个公式比较好求，但是得求出底面圆的半径，因为AB垂直于底面圆，在Rt△ABC中，由OC、AB＝BC、AC可求出r，问题就解决了．

解：在Rt△ABC中，AB＝13cm，AC＝5cm，

∴BC＝12cm．

∵OC·AB＝BC·AC，

∴r＝OC＝．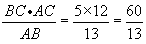

∴S_表＝πr(BC+AC)＝π×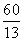×(12+5)

＝π cm²．

Ⅲ．课堂练习

随堂练习

Ⅳ．课时小结

本节课学习了如下内容：

探索圆锥的侧面展开图的形状，以及面积公式，并能用公式进行计算．

Ⅴ．课后作业

习题3．11

Ⅵ．活动与探究

探索圆柱的侧面展开图

在生活中，我们常常遇到圆柱形的物体，如油桶、铅笔、圆形柱子等，在小学我们已知圆柱是由两个圆的底面和一个侧面围成的，底面是两个等圆，侧面是一个曲面，两个底面之间的距离是圆柱的高．

圆柱也可以看作是由一个矩形旋转得到的，旋转轴叫做圆柱的轴，圆柱侧面上平行于轴的线段都叫做圆柱的母线．容易看出，圆柱的轴通过上、下底面的圆心，圆柱的母线长都相等，并等于圆柱的高，圆柱的两个底面是平行的．

如图，把圆柱的侧面沿它的一条母线剪开，展在一个平面上，侧面的展开图是矩形，这个矩形的一边长等于圆柱的高，即圆柱的母线长，另一边长是底面圆的周长，所以圆柱的侧面积等于底面圆的周长乘以圆柱的高．

[例1]如图(1)，把一个圆柱形木块沿它的轴剖开，得矩形ABCD．已知AD＝18cm，AB＝30cm，求这个圆柱形木块的表面积(精确到1cm²)．

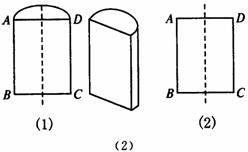
解：如图(2)，AD是圆柱底面的直径，AB是圆柱的母线，设圆柱的表面积为S，则S＝2S_圆+S_侧．

∴S＝2π(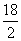)²+2π×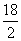×30＝162π+540π≈2204cm²．

所以这个圆柱形木块的表面积约为2204cm²．

板书设计

§3．8　 圆锥的侧面积

[师]圆锥的侧面展开图是一个扇形，如图，设圆锥的母线(generating line)长为l，底面圆的半径为r，那么这个圆锥的侧面展开图中扇形的半径即为母线长l，扇形的弧长即为底面圆的周长2πr，根据扇形面积公式可知S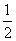＝·2πr·l＝πrl．因此圆锥的侧面积为S_侧＝πrl．

圆锥的侧面积与底面积之和称为圆锥的全面积(surfacearea)，全面积为S_全＝πr²+πrl．

[师](向学生展示圆锥模型)请大家先观察模型，再展开想象，讨论圆锥的侧面展开图是什么形状．

[生]圆锥的侧面展开图是扇形．

[师]能说说理由吗？

[生甲]因为数学知识是一环扣一环的，后面的知识是在前面知识的基础上学习的．上节课的内容是弧长及扇形面积，本节课的内容是圆锥的侧面积，而弧长不是面积，所以我猜想圆锥的侧面展开图应该是扇形．

[师]这位同学用的虽然是猜想，但也是有一定的道理的，并不是凭空瞎想，还有其他理由吗？

[生乙]我是自己实践得出结论的，我拿一个扇形的纸片卷起来，就得到了一个圆锥模型．

[师]很好，究竟大家的猜想是否正确呢？下面我就给大家做个演示(把圆锥沿一母线剪开)，请大家观察侧面展开图是什么形状的？

[生]是扇形．

[师]大家的猜想非常正确，既然已经知道侧面展开图是扇形，那么根据上节课的扇形面积公式就能计算出圆锥的侧面积，由于我们不能把所有圆锥都剖开，在展开图中的扇形的半径和圆心角与不展开图形中的哪些因素有关呢？这将是我们进一步研究的对象．

4．用一个半径长为6cm的半圆围成一个圆锥的侧面，则此圆锥的底面半径为　 (　　 )

　　 A．2 cm　 B．3 cm　 C．4 cm　 D．6 cm

　　 答案：1．D　 2．C　 3．C　 4．B

3．在半径为50 cm的图形铁片上剪去一块扇形铁皮，用剩余部分制做成一个底面直径为80 cm，母线长为50 cm的圆锥形烟囱帽，则剪去的扇形的圆心角的度数为(　　 )

　　 A．288°　 B．144°　 C．72°　　 D．36°

2．若一个圆锥的母线长是它底面圆半径的3倍，则它的侧面展开图的圆心角是(　　 )

　　 A．180°　　 B. 90°

　　 C．120°　　 D．135°