2.学生活动、意义建构、数学理论：

结合问题情景，思考：解决这个问题的关键是什么？题中涉及哪些量？这些量之间的关系如何？你能找出表示问题意义的相等关系吗？用方程怎样表达？

方法一：用直接未知数.设甲、乙两城市间的路程为x km，相等关系：提速前的运行时间－提速后的运行时间=缩短时间.

方法二：用间接未知数.设提速前列车从甲地到乙地的运行时间为x 小时，相等关系：提速前的运行速度×运行时间=提速后的运行速度×运行时间，即80x=100(x－3).

建议只让学生多一些方法，但不要讲的太多.

1.情景创设：

(1)列车提速问题，见课本P₁₁₅.

生活背景：从1997年到2004年，我国共进行了5次列车提速.

(2)见教师教学参考资料手机通讯话费付费方式

2.重、难点：分析问题，探寻等量关系列一元一次方程.

1.学习目标：

知识与技能：通过对具体实际生活问题的分析，进一步学会根据实际问题的意义设未知数并列出方程，了解一元一次方程的概念.

过程与方法：经历把实际问题抽象出数学问题的过程，体会方程是人们分析、解决实际问题的有效工具.

情感、态度与价值观：进一步领会方程与现实生活间的密切联系，感受数学建模思想的应用.

6.作业：见作业本。

5.课堂小结：

突出两条：一是什么叫做一个代数式的值？它与代数式的概念有什么不？二是求代数式的值的方法：先代入、后计算。

4.随堂练习：

　“练习”第 1， 2题。

在做完练习后，可启发学生思考：前两题在问法上有什么不同。可告诉学生，前一题求的是当字母取不同的数值时，同一个代数式的值；而后一题求的是当两个字母分别取定某个数值时，不同的代数式的值。

3. 再接着讲教科书上的例2，将它作为例3。

这个例子的代数式的分母里出现了字母，此处可顺便提一下，求一个代数式的值时，字母的取值应使代数式有意义，如本例里字母a的取值不能是0，以便为“小结与复习”里讲求代数式的值时的字母取值范围问题作一下铺垫。

2. 接着讲教科书上的例1。

在书写例1的求解过程时，可以加上“当x=7，y=4，z=0时”，以有利于弄清代数式的值的区别。本例中的代数式含有3个字母，可强调代入时一定要按照顺序进行，不要代错；代入之后，则要强调运算的顺序：在有括号的情况下，先进行括号内的运算；在进行括号内的运算时，则应遵循先乘除后加减的规定，在教科书上的两个例题中，未涉及含1个字母的代数式。实际上从函数的角度看，以后学习的函数主要还是一元函数。因此如果时间允许，可考虑在例1之后补充一个涉及1个字母的例题。

例 2当 a=2时，求代数式 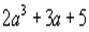　的值．

解：当 a=2时，

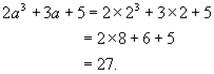
1. 先讲教科书第14页上的引入例，在这个涉及排球个数的代数式里，只含有一个字母。在此基础上可酌情补充一个含有两个字母的代数式的例子。

底是a厘米、高是h厘米的三角形的面积怎样表示？答：1/2ah(平方厘米)。然后，可根据这个代数式计算a，h分别取几个具体数值时的三角形的面积。

在上面例子的基础上，提出代数式的值的概念。

建议在提出代数式的值的概念后，再回到上面的例子作进一步说明。如指出当当n=15时，代数式2n+10的值是40，等等。此外，还要指出代数式与代数式的值的区别，不能笼统地说代数式的值是多少，而只能说，当字母取何值时，代数式的值是多少。