
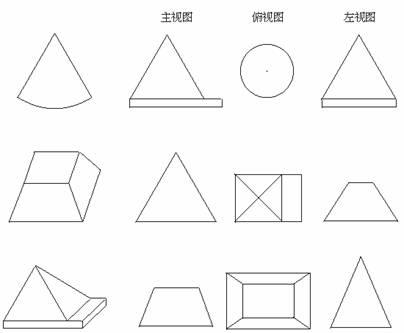
5.如图是一个物体的三视图,请画出物体的形状。
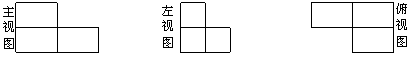
拓展创新 根据下面三视图建造的建筑物是什么样子的?共有几层?一共需要多少个小正方体。

4.画出右方实物的三视图。
3. 根据要求画出下列立体图形的视图。
根据要求画出下列立体图形的视图。
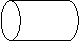

(画左视图) (画俯视图) (画正视图)

2.选择题
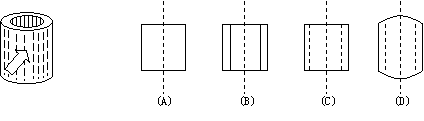
(1)圆柱对应的主视图是( )。




(A) (B) (C) (D)
 (2)某几何体的三种视图分别如下图所示,那么这个几何体可能是( )。
(2)某几何体的三种视图分别如下图所示,那么这个几何体可能是( )。
(A)长方体 (B)圆柱 (C)圆锥 (D)球
 (3)下面是空心圆柱在指定方向上的视图,正确的是…( )
(3)下面是空心圆柱在指定方向上的视图,正确的是…( )
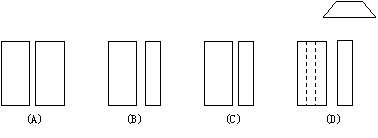 (4)一个四棱柱的俯视图如右图所示,则这个四棱柱的主视图和左视图可能是( )
(4)一个四棱柱的俯视图如右图所示,则这个四棱柱的主视图和左视图可能是( )
(5)主视图、左视图、俯视图都是圆的几何体是( )。
(A)圆锥 (B)圆柱 (C)球 (D)空心圆柱
第四章 视图与投影
§4.1 视图
§4.1.1 视图(一)
班级:__________ 姓名:__________
3.关于课本中“思考”的教学
安排“思考”的目的是让学生知道:
(1)数量变化的规律也可以用式子表示;
(2)用式子表示的数量间的变化关系可以用表格表示.
可以根据学生的实际情况,向部分学生提出挑战性的问题:你能设计一个折线图,表示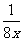 的数值随x的数值变化而变化的规律吗?
的数值随x的数值变化而变化的规律吗?
通过思考活动,引导学生进一步明确,实际问题中的数量常常会发生变化,表示这种变化通常有3种各具特色的表达方式--表格、图形、式子,可根据实际情况灵活选用;其次,面对一个实际问题,不论用哪一种方式表示数量的变化,都要重点关注数量变化的关系及规律.
2.探索活动
活动一:
先向学生简要介绍有关“城市化”的知识(参阅 [课程资源]),然后展示图片,通过问题串,引导学生从图片中发现数量变化的规律及相互间的关系,例如:
(1)看到这幅图片后,你获得的第一印象是什么?首先想要说的是什么?
(2)你能说出半个世纪以来,世界各国城市人口比重的变化情况吗?
(3)图中4国的城市人口比重的变化趋势有共同之处吗?
(4)日本的城市化进程与其他3国有何不同?
(5)你能就我国的城市化进程谈谈看法吗?
探索的目的不是寻求答案的统一,而是学会如何从图片提供的信息中,发现数量变化的大体规律,发现各变化的数量之间的共性与个性,给出预测和合理的解释.
活动二:
测肺活量是学生熟悉的情境,除了课本中的提问方式外,也可以提出以下问题,引导学生从图中获取数量变化的之间的关系:
(1)13岁男生的平均肺活量是多少?13岁的女生呢?它们的差异是多少?
(2)哪个年龄的肺活量最大?最大肺活量是多少?
(3)18岁男女学生的平均肺活量的差异是多少?
(4)哪个年龄段的男、女生肺活量差异较小?
(5)学生的肺活量随年龄增大而增大,这种变化在哪个年龄段最显著?
(6)你能说出肺活量随年龄变化而变化的一般规律吗?
1.情境创设
用图形表示变化的数量之间的关系,形象直观,便于比较.课本设计了以下两个情境:
(1)20世纪初期,西方主要国家都先后完成了城市化进程.东方国家的城市化进程大大落后于西方,只有日本进展较快.课本选取了中国、日本、印度、马来西亚4个国家城镇人口比重变化的折图线,情境简单,内涵丰富,应注意挖掘它的数学与人文两方面的教育价值.
(2)肺活量是评定学生体质的一项重要机能指标,课本用某校不同年龄的学生平均肺活量变化折线图,让学生感受年龄变化与肺活量变化的关系.如本校医务室有这样的折线图,教学中加以使用则更佳.
2.能根据图表所提供的信息,探索数量变化的某些联系.
此外,通过探索活动,感受生活中处处有变化的数量关系,并且这些变化的数量之间往往有一定的联系;感受用变化的观点分析数字信息的重要意义.
[教学过程(第二课时)]
1.会用表格、图形或数学式子记录、描绘或表示变化的数量;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com