1.学习目标：

知识与技能：了解与一元一次方程有关的概念，掌握等式的基本性质，能运用等式的基本性质解简单的一元一次方程.

过程与方法：经历数值代入计算的过程，领会方程的解和解方程的意义.知道求方程的解就是将方程变形为x=a的形式.

情感、态度与价值观：强调检验的重要性，养成检验反思的好习惯.

4.回顾反思：

(1)回顾去分母注意事项，见上面数学运用.(2)本课时蕴涵的数学思想方法主要是化归思想.解方程的过程就是通过去分母、去括号、移项、合并同类项、(未知数)系数化为1等步骤，把一个一元一次方程逐步转化为x=a的形式.这是一个等量变形的过程，也是一个化归的过程.(3)具体解方程时，可根据具体情况，有些步骤可能用不上；有些步骤可以前后顺序颠倒；有时还可以省略一些步骤，以使运算简化.

3.数学运用：

　　 结合情景问题的解法，师生互动处理课本P₁₂₃例7、例8.

　　 反馈矫正学生出现的问题，让学生展开讨论，发现解答时出错之处.

去分母时须注意：(1)确定各分母的最小公倍数；(2)不要漏乘没有分母的项；(3)分数线有括号作用，去掉分母后，若分子是多项式，要加括号，视多项式为一整体.建议进行专项训练，如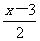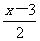，－乘以6，8……

概括解一元一次方程一般步骤，强调变形时各步易出现错误的内容.

习题练习：见课本P₁₂₄练一练1，2，3

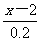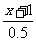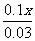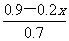思维拓展：见课本P₁₂₄议一议－=3；又如－=1

(提示：分子、分母是小数、分数的可以首先利用分数的基本性质将其化为整数系数，然后再解方程.)

2.学生活动、意义建构、数学理论：

由情景问题入手，引导学生审清题意，根据等量关系：学生总数的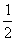+学生总数的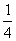+学生总数的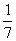+3＝学生总数列出方程.即设毕达哥拉斯的学生有x名，由题意得x/2+x/4+x/7+3＝x.

学生独立思考问题，尝试解方程，交流自己的解法，相互加以比较.

(生：①先移项再合并同类项；②先合并同类项后移项；③两边同时乘以28，56，84……)

学生比较上述方法，判断选择，引入--去分母.

1.情景创设：

毕达哥拉斯是古希腊著名的数学家，有一次有位数学家问他：“尊敬的毕达哥拉斯，请告诉我，有多少名学生在你的学校里听你讲课？” 毕达哥拉斯回答说：“我的学生，现在有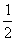在学习数学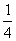，在学习音乐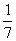，沉默无言，此外，还有三名妇女.”算一算：毕达哥拉斯的学生有多少名？

2.重、难点：利用“去分母”将方程作变形处理.

1.学习目标：

知识与技能：知道解一元一次方程的一般步骤，能灵活运用去分母、去括号、移项、合并同类项、系数化为1等五大步骤解一元一次方程.

过程与方法：巩固方程解法，经历求解过程，能体会到解法应根据具体方程本身特点而定.

情感、态度与价值观：体会化归思想--把复杂变简单，将未知变已知的作用，体会数学的应用价值.

4.2解一元一次方程3

题目 4.2解一元一次方程3 教学目标 经历和体会解一元一次方程中“转化”的思想方法 教学重点 会解带括号和分数的一元一次方程 教学难点 会解带括号和分数的一元一次方程 教学方法 引导发现式 教学工具 　 教学内容 教师活动 学生活动

复习提问： 移项 解方程　 －3(x+1)＝9 解1： 去括号得 　　　　　 －3x－3＝9 　　　 移项得 －3x＝9+3 合并同类项得 　　　　　 －3x＝12 　　　　 两边都除以－3，得 　 　　　　　x＝－4 解2： 两边都除以3得 　　　　 x+1＝－3 　　　 移项得 　　　　　 x＝－3－1 　　　　 合并同类项得 　　　　　 x＝－4 解方程　　 3(2x+5)=2(4x+3)－3　 　　　　　　 x＝6 解方程　　　　 ＝x+1 解： 两边都乘以6，得 　　　　　　 3(x+1)＝8x+6 　　 去括号，得 3x+3＝8x+6 　　　　 移项，得 　　　　　　 3x－8x＝6－3 　　　　 合并同类项，得 　　　　　　 －5x＝3 两边都除以5，得 　　　 x＝－ 解方程　 x－＝1 　　　　　　　 x＝ 讨论; 解一元一次方程的步骤？ 去分母 去括号 移项 合并同类项 未知数的系数化为1 练习： 6x―(x―4)=x―(2x+1) P157 1、2、3 作业： P157 2、4、5、6

4.回顾反思：

(1)学生从利用逆运算解方程到用移项法则解方程要有个过程，不宜操之过急.在移项时，学生常犯的错误是忘记变号，这主要是学生不熟悉移项法则，要对照等式的性质逐渐来理解.

(2)解例题时要不拘泥于课本上的解法，追求解题策略的多样化.另外，注意解题格式的规范化和检验的必要性.

(3)合并同类项法则学生可能已淡忘，适时进行整式的加减法的专项训练.教训：不要求学生“－x+2x=(－1+2)x=1x=x”谨小慎微，步子小了，也会拌自己的脚.

　　 (4)以练促讲，以练代讲.当堂检测，即时反馈.

3.数学运用：

课本P₁₂₀例2，P₁₂₁例3的教学处理：先让学生自主探求，师发问：解方程4x－15=9时，能否直接把等式左边的－15改变符号移到等式右边？方程4x－15=9与4x=9+15的差别在哪儿？解方程2x=5 x－21时，能否直接把等式右边的5 x改变符号移到等式左边？为什么？

指导学生在例2、例3解方程的过程中发现规律，结合两例课本云图说明及卡通人的介绍，引出这种方程的变形是移项.学生自主总结出移项法则--移项要变号. 牢记：从等式左边移到等式右边的项要变号；从等式右边移到等式左边的项也要变号.“叛变”了嘛！

建议补充什么是多项式的项，未知项，常数项？

用移项法解方程须注意：

(1)目标明确，解方程目标是把方程变形为x=a的形式；

(2)移项时，要移谁，移到哪？

(3)怎样移项？方法一是利用加、减法互逆运算这一关系；方法二是利用等式的性质；方法三是移项法则.

用课本P₁₂₁例4来进一步熟悉移项法则在解方程中的运用.注意解题步骤的规范化.

习题训练：(1)以下移项变形是否正确？(2)解方程，如课本P₁₂₂练一练1，2等.

思维拓展，解简单的应用题，如课本P₁₂₂练一练3或补充一些题.