
x2+5x+2=0.
解:把常数项移到方程的右边,得
x2+5x=-2.
两边都加上(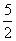 )2,得
)2,得
x2+5x+(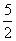 )2=-2+(
)2=-2+(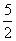 )2,
)2,
即(x+ 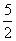 )2=
)2=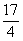 .
.
两边同时开平方,得
x+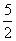 =±
=±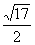 ,
,
即x+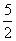 =
=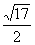 或x+
或x+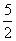 =-
=-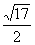 .
.
所以x1=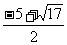 ,x2=
,x2=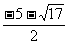 .
.
设计方案一:
设计方案二:
设计方案三:
设计方案四:
x2+12x=15,
x2+12x+62=15+62,
即(x+6)2=51,
x+6=±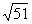 ,
,
即x+6=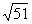 或x+6=-
或x+6=-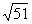 ,
,
x1=-6+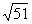 ,x2=-6-
,x2=-6-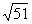 (舍).
(舍).
梯子底端滑动的距离是(-6+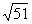 )米.这种解一元二次方程的方法称为配方法.
)米.这种解一元二次方程的方法称为配方法.
例1:解方程x2+8x-9=0
x=±2.
(2)(x+3)2=9,
x+3=±3,
x+3=3或x+3=-3,
x1=0,x2=-6.
这种方法叫直接开平方法.
(x+m)2=n(n≥0).
备课资料
参考例题
例1:用分解因式法解下列方程:
(1)(2x-5)2-2x+5=0;
(2)4(2x-1)2=9(x+4)2.
分析:方程(1)的左边化为以(2x-5)为整体的形式,然后利用提取公因式来分解因式;方程(2)先移项,然后将(2x-1)和(x+4)看作整体,利用平方差公式分解因式.
解:(1)方程化为(2x-5)2-(2x-5)=0,
(2x-5)[(2x-5)-1]=0.
∴2x-5=0或(2x-5)-1=0.
∴x1=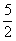 ,x2=3.
,x2=3.
(2)方程化为
4(2x-1)2-9(x+4)2=0,
[2(2x-1)+3(x+4)][2(2x-1)-3(x+4)]=0.
∴2(2x-1)+3(x+4)=0,
2(2x-1)-3(x+4)=0.
∴x1=-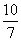 ,x2=14.
,x2=14.
例:解下列方程;
(1)5x2=4x;
(2)x-2=x(x-2).
解:由方程x2=3x得
x2-3x=0,
即x(x-3)=0.
于是x=0或x-3=0.
因此,x1=0,x2=3.
所以这个数是0或3.
两边都除以2,得
x2-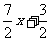 =0.
=0.
移项,得
x2- .
.
配方,得
x2-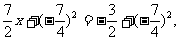
(x- .
.
两边分别开平方,得
x- ,
,
即x- 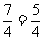 或x-
或x-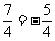 .
.
∴x1=3,x2=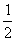 .
.
6.布置作业
课本P125 T7
|
2.已知一个数的3倍与2的差等于它的2倍与3的和,求这个数.
课堂小结:
.
作业布置:课时作业本P57解一元一次方程(二)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com