
P87 练习1、2 P93 习题4.2 2、3
2、用配方法解一元二次方程的一般步骤是什么?
引导学生总结:
1、配方法解一元二次方程的作用是什么?配方时要注意什么?
P87 练习 1、2、3
3、利用直接开平方法解之。
思考:为什么在配方过程中,方程的两边总是加上一次项系数一半的平方?
2、在方程的两边各加上一次项系数的一半的平方,使左边成为完全平方;
例 1 将下列各进行配方:
⑴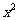 +8x+_____=(x+_____)2
⑵
+8x+_____=(x+_____)2
⑵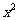 -5x+_____=(x-_____)2
-5x+_____=(x-_____)2
⑶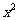 -
-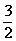 x+_____=(x-____)2
⑷
x+_____=(x-____)2
⑷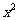 -6
-6 x+_____=(x-____)2
x+_____=(x-____)2
分析:本题应用“方程两同时加上一次项系数一半的平方”来配方。
例 2 解下列方程:
(1) x2-4x+3 = 0 (2)x2+3x-1 = 0
小结:用配方法解一元二次方程的一般步骤:
1、把常数项移到方程右边;
我们能否将方程x2+6x+4 = 0转化为(x+m)2= n的形式呢?
先将常数项移到方程的右边,得
x2+6x = -4
即 x2+2·x·3 = -4
在方程的两边加上一次项系数6的一半的平方,即32后,得
x2+2·x·3 +32 = -4+32
(x+3)2 = 5
解这个方程,得
x+3 = ±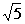
所以 x1 = ―3+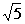 x2
= ―
x2
= ―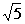
(注:可以多举几例,综合得出“两边加上一次项系数一半的平方”的结论)
由此可见,只要先把一个一元二次方程变形为(x+m)2= n的形式(其中m、n都是常数),如果n≥0,再通过直接开平方法求出方程的解,这种解一元二次方程的方法叫做配方法。
我们已经学过了用直接开平方法解形如(x+m)2= n(n≥0)的一元二次方程,那么如何解方程x2+6x+4 = 0呢?
P88 练习1 P93 习题4.2 3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com