4．一个人的生日是周日的概率为　　　　 ，两个人的生日都是星期日的概率为　　　　 ，两个人的生日是一周中同一天的概率为　　　　 ．

3．用图两个转盘进行“配紫色”游戏，配成紫色的概率是　　　 　．

2．连续掷硬币两次，其中两次结果相同的概率为　　　　 ，两次正面朝上的概率为　　　　　 ．

1．从一幅扑克牌中任取一张，是梅花的概率为　　　　 ．

2．小明和小芳用如下转盘图进行配紫色游戏，分别转动两个转盘，若配成紫色则小明得1分，否则小芳得1分，这个游戏对双方公平吗？如果你认为不公平，如何修改得分规则才能使游戏对双方公平？

1．小东和小明设计了两个掷骰子的游戏，每个游戏每次都是掷两枚骰子．

游戏一：和为7或者8，则小东得1分；和是其他数字，小明得1分．

游戏二：和能够被3整除，小东得3分；和不能被3整除，小明得1分．

这两个游戏公平吗？说说你的理由；若不公平，你能将它们改为公平吗？

[例1]　 某一家庭有两个孩子，请问这两个孩子是一个男孩一个女孩的概率是多少？你是怎样知道的．

[例2]　 在掷骰子的游戏中，当两枚骰子的和为质数时，小明得1分，否则小刚得1分．你认为该游戏对谁有利？如果当两枚骰子的点数之和大于7时，小刚得1分，否则小明得1分呢？

[例3]　 乘火车从A站出发，沿途经过3个车站方可到达B站，那么在A、B两站之间需要安排　　 种不同的车票．

[例4]　 某班53名学生右眼视力(裸视)的检查结果如下表所示：

则该班学生右眼视力的中位数是　　　　 ．如果右眼视力在0．6以下(不含0．6)的同学都戴着眼镜，那么从中任意抽取1名学生戴着眼镜的概率为　　　　 ．

[例5]　 小刚考试得了第一名，老师决定以精美的书作为奖励．现有3本书，老题告诉他，这三本书事先已给予了编号1，2，3(该编号只有老师知道)，小刚可以从3本书中任挑一本；也可以把这三本书给以排序，自左向右的排列序号与书的编号一致的书，小明均可得到，但若排列号与书的编号没有一致的，则一本书也得不到．小刚当然想多得到几本书，他该如何选择呢？请你帮他出个主意．

2．当两枚骰子的点数之积为奇数时，小刚得1分，否则小明得1分．这个游戏对双方公平吗?为什么?

　　 [生]如果我是小明，我一定会很高兴．

　　 [师]为什么呢?

　　 [生]因为这个游戏对小刚很不利．由上面的表格可求得小刚获胜的概率为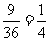，小明获胜的概率为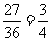.因此小明获胜的概率大．

　　 [师]可是玩了几次后，小刚发现上面游戏(2)的规则对自己不公平，于是小明说：“那这样，当两枚骰子的点数之积为奇数时，你得2分，否则我得1分”，你认为小刚应当接受这个规则吗?

　　 [生]我是小刚就不能接受，尽管小明让步，但此游戏规则对小刚还是不利．

　　 [师]大家认为如何修改规则，才能使游戏双方公平呢?

　　 [生]游戏规则可以修改为：当两枚骰子的点数之积为奇数时，小刚得3分，否则小明得1分．

　　 [师]谁还能有别的方法修改游戏规则，使游戏双方公平呢?

　　 [生]当两枚骰于的总数之和小于7时，小刚得1分，大于7时，小明得1分，等于71时，小刚和小明都不得分．这样小刚和小明获胜的概率都为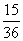．这样这个游戏规则对双方都是公平的．

　　 [师]我们常玩的游戏除了掷骰子外，还有“配紫色”游戏，下面我们一同再来做下面的游戏．

做一做

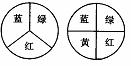
用下图中两个转盘进行“配紫色”游戏.

分别旋转两个转盘，若其中一个转盘转出了红色，另一个转出了蓝色，则可配成紫：色，此时小刚得1分，否则小明得1分．

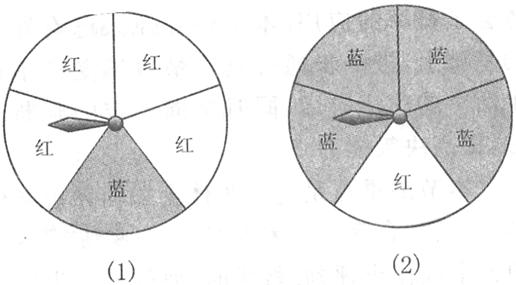
这个游戏对双方公平吗?若你认为不公平，如何修改规则，才能使该游戏对双方公平呢?

[生]为了保证自由转动转盘，指针落在每个区域的可能性相同，我们把转盘(1)按逆时针把红色区域等分成四部分，分别记作红1、红2、红3、红4，转盘(2)也类似地把蓝色区域分别记作蓝1、蓝2、蓝3、蓝4．接下来，我们就可以用列表法计算分别旋转两个转盘，其中一个转盘转出红色，另一个转出蓝色可配成紫色的概率．列表如下：

第二个转盘出的颜色 　 　 第一个转盘转出颜色	蓝1	蓝2	蓝3	蓝4	红色
红1	√	√	√	√	×
红2	√	√	√	√	×
红3	√	√	√	√	×
红4	√	√	√	√	×
蓝色	×	×	×	×	√

注，“√”表示可配成紫色，“×”表示不可配成紫色．

分别转动两个转盘，可配成紫色的概率为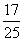，不可配成紫色的概率为.

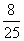因此，这个游戏对双方不公平，对小明不利.

　　 [师]你会想什么办法，修改规则才能使游戏对双方公平呢?

　　 [生]分别旋转两个转盘，配成紫色，则小刚得8分，否则小明得17分，这样可以表示游戏公平．

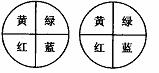
　　 [师]、明也发现了最开始的规则对自己不利．因此，他建议改用同一个转盘转动两次做“配紫色”游戏．小刚想，这没有什么区别，便欣然同意了小明的提议．你认为小刚的决策明智吗?

　　 [生]用第一个转盘转两次，配成紫色的概率我们还用列表法来计算．列表如下：

第二个转盘出的颜色 　 　 第一个转盘转出颜色	蓝1	蓝2	蓝3	蓝4	红色
红1	×	×	×	×	√
红2	×	×	×	×	√
红3	×	×	×	×	√
红4	×	×	×	×	√
蓝色	√	√	√	√	×

备注：“√”表示配成紫色，“×”表示不能配成紫色．

　　 由所列表格可知转动第一个转盘两次，配成紫色的概率为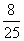，配不成紫色的概率为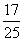，因此小刚的决策不明智．

　　 [师]如果把第(2)个转盘自由转动两次，配成紫色的概率为多少呢?

　　 [生]也用列表的方法可以计算出配成紫色的概率为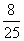，配不成紫色的概率为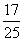．小刚的决策还是不明智．

　 　Ⅲ．随堂练习

　　 积极参与数学活动，在活动中获得成功的喜悦，提高学习数学的兴趣．

教学重点

　　 通过具体问题情境，让学生进一步体会如何评判某件事情是否“合算”，并利用它对一些游戏活动的公平性作出评判．

教学难点

　　 通过概率的知识解释游戏的公平性．

教学方法

引导--探究法

教具准备

骰子，转盘等．

教学过程

　　 Ⅰ.了解概率统计的一些应用，创设问题情境，建立“活动”平台

　　 我们在生活中常做一些游戏，但游戏规则的制定必须对双方都是公平的，这个游戏才能进行，否则就会有一方因为游戏不公平而退出游戏，下面我们就来看一例．

　　 Ⅱ．讲授新课

　　 [师]小明和小刚正在做掷骰子的游戏．两人各掷一枚骰子．

1．当两枚骰子的点数之和为奇数时，小刚得1分，否则，小明得1分，这个游戏对双方公平吗?

　　 [生]我认为游戏对双方公平．

　　 [师]游戏怎样才算公平呢?

　　 [生]只要，双方获胜的概率相等，也就是说双方获胜的可能性一样，就认为游戏对双方是公平的．

　　 [师]小刚获胜的概率是多少呢?

　　 [生]小刚获胜的概率就是两人各掷一枚骰子，当两枚骰子总数之和为奇数时的概率．我们在前面曾学习过计算概率的方法--树状图．列表法．

　　 [师]很好!下面就请同学们用列表法来求小刚获胜的概率．

　[生]列表如下：

根据表格可知小刚获胜的概率为．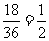

　　 [师]小明获胜的概率如何求呢?

　　 [生]小明获胜的概率即两枚骰子的点数之和为偶数的概率，由上面的表格也可求得为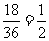

　　 [师]上面两个同学的回答已经告诉我们小刚和小明做的游戏对双方是公平的，但是小刚玩了一会儿，觉得这种玩法没意思，又想出了另外一种玩法．