
2.重、难点:利用“去分母”将方程作变形处理.
1.学习目标:
知识与技能:知道解一元一次方程的一般步骤,能灵活运用去分母、去括号、移项、合并同类项、系数化为1等五大步骤解一元一次方程.
过程与方法:巩固方程解法,经历求解过程,能体会到解法应根据具体方程本身特点而定.
情感、态度与价值观:体会化归思想--把复杂变简单,将未知变已知的作用,体会数学的应用价值.
2. 探索解决问题
(1)设爷爷跑步的速度是xm/min,那么可以列出表格
|
|
速度(m/min) |
时间(min) |
路程(m) |
|
爷爷 |
x |
5 |
5x |
|
小红 |
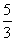 x x |
5 |
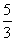 x x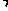 5 5 |
(2) 
 “线段图”表示
“线段图”表示

 小红跑的路程
小红跑的路程





 爷爷跑的路程, 400
爷爷跑的路程, 400
学生利用所学知识自己尝试分析,教师提示:这个问题可以用列表和画示意图的方法来分析,试试看.你借助分析过程能得出问题的相等关系吗?根据相等关系如何列方程,把你的想法与大家交流.



 分析:(1)
分析:(1) 

 400m
400m
 (2)“线段图”表示:
(2)“线段图”表示:
 小红跑的路程
小红跑的路程 




 爷爷跑的路程 300m
爷爷跑的路程 300m  2h
2h
|
1. 提出问题:
(1)参加过学校运动会800m或1500m的比赛项目吗?速度快的人与速度慢的人会相遇吗?第一次相遇他们各自所走的路程之间有什么关系?
(2)从同一地点出发往同一方向行走,小红5分钟后第一次追上了爷爷,他们所走的路程之间有什么关系?
3.数学运用:
例题见课本P132问题4.
运动场跑道周长400m,小红跑步的速度是爷爷的倍,他们从同一地点沿跑道的同一方向同时出发,小红5分钟后第一次追上了爷爷,你知道他们的跑步速度吗?
4.回顾反思:
(1)解方程,读懂题意是解决问题的前提,审题不要留于形式,“磨刀不误砍材工”.
(2)所谓解题建模策略,是帮助学生理解题意,找清楚各量间的关系的一种方法,一种策略,一种途径,一个手段,不要过多地加大对解题策略(列表格)的分析、构建,这不应成为解方程的新的难点.学习时,可用列表格法表示问题的数量关系,列出代数式,帮助理清思路,找准等量关系列方程.
|
3.数学运用:
课本P129问题2.
学生仔细审题(齐读或精读后能复述题意)思考:(1)指出问题中的数、数量、已知数量和未知数量;(2)表格可以怎样设计?(3)设小丽买了xkg苹果,如何用表格分析问题中的数量关系?列出方程是什么?
思维拓展:本题还有没有其它解法?
(如:设小丽买了xkg橘子;设小丽买了x元苹果;设小丽买了x元橘子)
|
|
价格(元/kg) |
质量/kg |
总金额/元 |
|
苹果 |
3.2 |
|
|
|
橘子 |
2.6 |
|
|
教师小结,让学生体会用方程解决问题时,设未知数的方法不同,方程的复杂程度也常常不同,因此要有所选择.
习题练习:见课本P130练一练2,3.
1.某面粉仓库存放的面粉运出 15%后,还剩余42 500千克,这个仓库原来有多少面粉?
|
5.练习反馈:
4.回顾反思:
(1)进一步熟悉解一元一次方程的方法步骤;
(2)弄清楚用一元一次方程解决问题的关键;
(3)根据学生情况,适当补充安排较多类型的问题.如课本P129练一练3,4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com