3.2x+2.6y=18　　

(第三种解法如果有学生给出，教师要给以积极的鼓励)

　　 本节课以分析问题中的数量关系为主，故求方程的解不作为本节课重点，但为了激励学生多角度思考，可求出解1、解2以验证两种解法的正确性。但要提示学生：设未知数的方法不同，方程的复杂程度也常常不同，因此要有选择。

教师小结：今天用方程解决的问题比较复杂，为了更好的理清问题中的数量关系，我们常用列表的方法来帮助我们解决问题。

3.2x + 2.6(6-x) = 18　　　　　　　　　　 2.6x + 3.2(6-x) = 18

解3：设小丽买苹果x kg,则买橘子y kg.　

根据题意得：　 x+y=6　　　　　

2、议一议：(主要围绕下面两个问题展开)

①如何设未知数？

②根据什么等量关系列方程？

[在讨论第一个问题时，根据学生的思维老师写出相应的板书，其中有的学生可能会设两个未知数，老师在教学中要给以肯定和鼓励；讨论第二个问题时，老师要引导学生分析等量关系式的左、右两边还需要那些代数式，再列出方程。(为学习列表埋下伏笔)]

板书如下：

解1：设小丽买苹果x kg,则买橘子(6-x) kg.　 解2：设小丽买橘子x kg,则买苹果(6-x) kg

根据题意，得；　　　　　　　　　 根据题意，得：

2、在这些步骤中，关键是什么？

(根据学生的回答用彩笔标出第二步，以引起注意)

1、回忆上节课的内容，结合下列问题思考：

用方程解决问题的一般步骤是什么？

(投影揭示问题)

小明在暑假去桂林旅游5天，这5天的日期之和是20。小明是几号出发的？

　 (此题虽是为复习上节课的内容而设，但涉及了连续几个整数的表示方法，因而可让学生独立思考或小组讨论后进行交流，教师根据学生回答进行板书)

　　 　步骤1：　 用字母表示　 　　　　解：设小明是x号出发的，则后四天分

　　 　　　适当的未知数　 　　　　　　别为(x+1)、(x+2)、(x+3)、(x+4)号。

　　 　步骤2： 根据题中的　　 　　　　　　根据题意，得：

相等关系列出方程　　 　　　　　　x +(x+1)+(x+2)+(x+3)+(x+4) = 20

　步骤3：解方程求出　　 　　　　　　解这个方程，得

　　　 　　未知数的值　　　　 　　　　　　x = 2

步骤4：问题的答案　 　　　　　　答：小明是 2 号出发的

4.回顾反思：

(1)回顾去分母注意事项，见上面数学运用.(2)本课时蕴涵的数学思想方法主要是化归思想.解方程的过程就是通过去分母、去括号、移项、合并同类项、(未知数)系数化为1等步骤，把一个一元一次方程逐步转化为x=a的形式.这是一个等量变形的过程，也是一个化归的过程.(3)具体解方程时，可根据具体情况，有些步骤可能用不上；有些步骤可以前后顺序颠倒；有时还可以省略一些步骤，以使运算简化.

3.数学运用：

　　 结合情景问题的解法，师生互动处理课本P₁₂₃例7、例8.

　　 反馈矫正学生出现的问题，让学生展开讨论，发现解答时出错之处.

去分母时须注意：(1)确定各分母的最小公倍数；(2)不要漏乘没有分母的项；(3)分数线有括号作用，去掉分母后，若分子是多项式，要加括号，视多项式为一整体.建议进行专项训练，如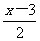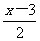，－乘以6，8……

概括解一元一次方程一般步骤，强调变形时各步易出现错误的内容.

习题练习：见课本P₁₂₄练一练1，2，3

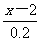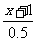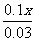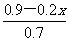思维拓展：见课本P₁₂₄议一议－=3；又如－=1

(提示：分子、分母是小数、分数的可以首先利用分数的基本性质将其化为整数系数，然后再解方程.)

2.学生活动、意义建构、数学理论：

由情景问题入手，引导学生审清题意，根据等量关系：学生总数的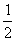+学生总数的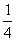+学生总数的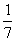+3＝学生总数列出方程.即设毕达哥拉斯的学生有x名，由题意得x/2+x/4+x/7+3＝x.

学生独立思考问题，尝试解方程，交流自己的解法，相互加以比较.

(生：①先移项再合并同类项；②先合并同类项后移项；③两边同时乘以28，56，84……)

学生比较上述方法，判断选择，引入--去分母.

1.情景创设：

毕达哥拉斯是古希腊著名的数学家，有一次有位数学家问他：“尊敬的毕达哥拉斯，请告诉我，有多少名学生在你的学校里听你讲课？” 毕达哥拉斯回答说：“我的学生，现在有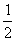在学习数学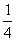，在学习音乐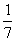，沉默无言，此外，还有三名妇女.”算一算：毕达哥拉斯的学生有多少名？