
4.3用方程解应用题2
|
|||||||||||||||
|
4.3用方程解应用题 1
|
|||||||||||||||
|
4.回顾反思:
应用题的类型和每个类型所用到的基本数量关系(仅作参考)
(1)等积类:变形前的体积(容积)=变形后的体积(容积);
(2)调配类:注意调配前的数量关系,调配后的数量关系;
(3)利息类:本息和=本金+税后利息,税后利息=本金×利率×80%;
(4)商品销售类:利润率=利润/进价,利润=售价-进价;
(5)工程类:工作量=工作时间×工作效率;
(6)行程类:路程=速度×时间①相遇问题:总路程=甲走的路程+乙走的路程;追及问题:追者走的路程=前者走的路程+两地间的路程;②环形跑道问题:“同时同地同向出发:快的多跑一圈才能追上慢的;同时同地反向出发:两人第一次相遇时的总路程为环形跑道一圈的长度.”③航行问题:顺水速度=静水速度+水速;逆水速度=静水速度-水速;顺水速度-逆水速度=2×风速;
(7)比例类:若甲、乙的比是3:5,可设甲为3x,乙为5x;
(8)数字类:若一个三位数,百位数字为a,十位数字为b,个位数字为c,则这个三位数可表示为:100a+10b+c.
3.数学运用:
例:某种商品因换季准备打折出售,如果按定价的七五折出售将赔25元;而按定价的九折出售将赚20元.问这种商品的定价是多少?(0.75x+25=0.9x-20,x=300)
学生独立思考,解决问题.
习题练习:见课本P136练一练1,2. P137 14,P138 15.
思维拓展:见课本P136试一试.
2.学生活动、意义建构、数学理论:
分析:本题含有明显的等量关系是利润=售价-进价.
学生思考:设这种皮装的进价为每件x元,则标价应是 元,售价为 元,列方程是 .
解:设这种皮装的进价为每件x元,根据题意得x×150%×80%-x=160;
解这个方程得x=800.
答:略.
学生自读课本P135问题6,比较与情景问题的区别、联系.进一步理解示意图的作用.
1.情景创设:
某商场在销售一种皮装时,为了吸引顾客,先按进价的150%标价,再按标价的8折(标价的80%)出售,结果每件皮装仍获利160元,问这种皮装的进价为每件多少元?
2.重、难点:理清标价、折扣率、利润(率)、售价等数量之间的关系,找准等量关系.
1.学习目标:
知识与技能:理解商品销售中的进价、标价、折扣率、利润(率)、售价等概念及其之间的关系.能根据利润=实际售价一进价等数量关系列一元一次方程求解.
过程与方法:进一步体会方程模型的作用,,总结运用方程解决实际问题的一般方法,提高应用数学的意识.
情感、态度与价值观:通过商品销售的学习,使学生认识到数学的应用价值,通过获得成功的体验和克服困难的经历,增进应用数学的自信心.
4.回顾反思:
(1)回顾去分母注意事项,见上面数学运用.(2)本课时蕴涵的数学思想方法主要是化归思想.解方程的过程就是通过去分母、去括号、移项、合并同类项、(未知数)系数化为1等步骤,把一个一元一次方程逐步转化为x=a的形式.这是一个等量变形的过程,也是一个化归的过程.(3)具体解方程时,可根据具体情况,有些步骤可能用不上;有些步骤可以前后顺序颠倒;有时还可以省略一些步骤,以使运算简化.
3.数学运用:
结合情景问题的解法,师生互动处理课本P123例7、例8.
反馈矫正学生出现的问题,让学生展开讨论,发现解答时出错之处.
去分母时须注意:(1)确定各分母的最小公倍数;(2)不要漏乘没有分母的项;(3)分数线有括号作用,去掉分母后,若分子是多项式,要加括号,视多项式为一整体.建议进行专项训练,如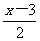 ,-
,-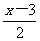 乘以6,8……
乘以6,8……
概括解一元一次方程一般步骤,强调变形时各步易出现错误的内容.
习题练习:见课本P124练一练1,2,3
思维拓展:见课本P124议一议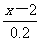 -
-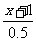 =3;又如
=3;又如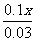 -
-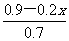 =1
=1
(提示:分子、分母是小数、分数的可以首先利用分数的基本性质将其化为整数系数,然后再解方程.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com