2．探索活动
可以提出一些实际问题，引导学生将实际问题数学化．例如：
(1)小亮是怎样描述音乐喷泉的位置的?
(2)小亮可以省去“西边”和“北边”这几个字吗?
(3)如果小亮说在“中山北路东边、中山东路北边”，小丽能找到音乐喷泉吗?
(4)如果小亮只说在“中山北路西边50m”，小丽能找到音乐喷泉吗?只说在“北京西路北边30m”呢?
通过研讨，交流，学生充分感受只有按课本中小亮的说法，小丽才能很容易地找到音乐喷泉的位置．
1．情境创设
创设情境的目的，是让学生感受确定点的位置是实际问题的需要．因此，除课本设计的情境外，可以选用学生熟悉的其他例子．例如，家庭住址、电影院的座位、图书馆里某本书的位置等．
4．能建立适当直角坐标系，将实际问题数学化，并会用直角坐标系解决问题．
此外，通过探索活动，让学生进一步感受“数形结合”的数学思想，感受“类比”和“坐标”的思想．体验将实际问题数学化的过程与方法．
[教学过程(第一课时)]
本课时从实例引进平面直角坐标系及其有关概念．
3．在同一直角坐标系中，探索位置变化与数量变化的关系、图形位置的变化与点的坐标变化的关系．
2．会在给定的直角坐标系中，根据点的坐标描出点的位置，会由点的位置写出点的坐标．
1．领会实际模型中确定．位置的方法，会正确画出平面直角坐标系．
4.3平面直角坐标系
[教学目标]
4.3用方程解应用题(4)
|
|||||||||||
|
3.14 x =720 x = 229.2…» 230
(5)检验求得的值是否正确和符合实际情形，并写出答案：应截取圆 钢的长为230毫米。
作业：
1一件工作，甲单独做6小时完成，乙单独做12小时完成，丙单独做18小时完成，若先由甲、乙合做3小时，然后由乙丙合做，问共需几小时完成？
2一件工程，甲、乙两人合作6天完成，甲独做10天完成，现在甲独做若干天后，由乙接替甲将剩余的部分完成，这样两人共用了12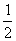
天，问甲乙两人各工作了几天？
3甲、乙两部抽水机共同灌溉一块稻田，5小时可以完成任务的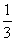
。已知甲抽水机3小时的抽水量等于乙抽水机5小时的抽水量，甲、乙抽水机单独灌溉这块稻田各需几小时？
4已知一圆柱形容器底面半径为5dm,高线长为1.5m,里面盛有1m深的水，将底面半径为3dm，高线长为0.5m的圆柱形铁块沉入水中，问容器内水面将升高多少
|
4.3用方程解应用题3
|
|||||||||||
|
小时)的时间把一个紧急通知传到队长那里。通讯员必须以怎样的速度行进？
根据题意，得方程：
小时，逆风飞行用了6小时．求这次飞行的风速？
－
＝
－
＝1
+
=1
+
＝1
+