4.已知线段AB=2cm，延长AB到C，使BC=2AB，若D为AB的中点，则线段DC的长为______.

3.如下图，线段AC=BD，那么AB=_____.

2. 要在墙上钉一根水平方向的木条，至少需要_____个钉子，用数学知识解释为____________________．

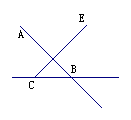
1. 中画出的直线有_____条，分别是________．

3.数学运用：

⑴课本P₁₀₂问题1：

分析：根据题中关键语句“做这批桌子，恰好用去木材3.8m³”，得相等关 系：做桌面的木材+做桌腿的木材=3.8m³.设共做了x张桌子，做桌面的木

材需0.03x m³，做桌腿的木材需4×0.002x m³，方程为0.03x+4×0.002x

=3.8……学生自主解决问题.

习题练习：课本P₁₀₂练一练1，2；　　　　　　　　　　　　　　　　　　　

　思维拓展：数学实验室(月历问题)，下图提供2005年11月的月历表

问题(1)(2)见课本P₁₀₂；

根据“数学实验室”中的游戏，请你再编一个游戏，并列出方程求解.如：

①某列3个数的和为54，这3个数是几？和能为56吗？②月历中能有2×

2矩形方块中的4个数之和为80吗？若有，这四个数之间有怎样的关系？

回顾反思：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 修改意见

①进一步让学生熟悉解一元一次方程的方法步骤；

②让学生弄清楚用一元一次方程解决问题的关键；

⑵课本P₁₀₃问题2：

学生仔细审题(齐读或精读后能复述题意)思考：(1)指出问题中的数、

数量、已知数量和未知数量；(2)表格可以怎样设计？(见下表)(3)设

小丽买了xkg苹果，如何用表格分析问题中的数量关系？列出方程是什么？

思维拓展：本题还有没有其它解法？

教师小结：让学生体会用方程解决问题时，设未知数的方法不同，方程的

复杂程度也常常不同，因此要有所选择．

习题练习：见课本P₁₀₄练一练2，3．(只列方程)

回顾反思：

(1)　　　 列方程解决问题，读懂题意是解决问题的前提，审题不要留于形式，

“磨刀不误砍材工”．

(2)所谓解题建模策略，是帮助学生理解题意，找清楚各量间的关系的一

种方法，一种策略，一种途径，一个手段，不要过多地加大对解题策略

(列表格)的分析、构建，这不应成为解方程的新的难点.学习时，可用列

表格法表示问题的数量关系，列出代数式，帮助理清思路，找准等量关系

列方程．

⑵课本P₁₀₄问题3：

借助线形示意图分析相等关系

学生思考：根据问题中的第②个条件，这个小组计划做的中国结多少个？

怎样在示意图上表示？你能根据示意图中线段和或差写出相等关系吗？

并根据相等关系列出方程吗？ 解决这个问题还有其他方法吗？

习题练习：见课本P₁₀₅练一练2，3，4(3，4只列方程)

回顾反思：

线形示意图通常可以画成直线图或环形图等，用线段的长或曲线的长来表

示某些量，并根据这些线段或曲线的长度关系列出方程．行程类问题中的

数量关系多数可以用示意图来表达．

2.学生活动、意义建构、数学理论：

借用课本中两个卡通人的对话，学生思考：(1)如果用算术解法你能解出

结果吗？如何求？(2)若用方程求解，如何设未知数？等量关系式是什

么？(3)如果在三色冰淇淋中，咖啡色、红色和白色配料比是2∶3∶5，

那么如何设未知数？

1.情景创设：冰淇淋配料问题，见课本P₁₀₂.

质量为45g的某种三色冰淇淋中，咖啡色、红色和白色配料的

比为1∶2∶6，这三色冰淇淋中咖啡色、红色和白色配料分别是多少？

2、小明中考时的准考证号码是由四个数字组成的，这四个数字组成的四位数有如下特征：(1)它的千位数字为1；(2)把千位上的数字1向右移动，使其成为个位数字，那么所得的新数比原数的5倍少49.请你根据以上特征推出小明的准考证号码.

1、两根同样长的蜡烛，点完一根粗蜡烛要2小时，而点完一根细蜡烛要1小时.一天晚上停电，明明同时点燃了这两支蜡烛看书，若干分钟后来电了，明明将两芝蜡烛同时熄灭，发现粗蜡烛的长是细蜡烛的2倍，问：停电多少分钟？

3、一个两位数，个位数字是十位数字的4倍，把个位数字与十位数字对调，得到的两位数比原来大54，求原数.

[知能升级]