
8、探究余角的性质:
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
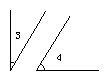
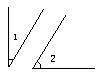
教师活动:操作多媒体演示。
学生活动:观察图形的运动,得出结果:∠2=∠4
余角性质:同角或等角的余角相等
教师活动:向学生说明,以上从观察图形得到的结论,还可以从理论上说明其理由。
∵ ∠1 +∠2=90°, ∠3 +∠4=90°
∴ ∠2=90°-∠1 , ∠4=90°- ∠3
∵ ∠1 =∠3
∴ 90°-∠1 =90°- ∠3
即:∠2 =∠4
7、探究补角的性质:
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
教师活动:操作多媒体演示。
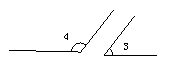
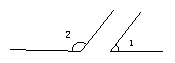
学生活动:观察图形的运动,得出结果:∠2=∠4
补角性质:同角或等角的补角相等
教师活动:向学生说明,以上从观察图形得到的结论,还可以从理论上说明其理由。
∵ ∠1 +∠2=180°, ∠3 +∠4=180°
∴ ∠2=180°-∠1 , ∠4=180°- ∠3
∵ ∠1 =∠3
∴ 180°-∠1 =180°- ∠3
即:∠2 =∠4
6、练习⑶:
一个角的补角是它的3倍,这个角是多少度?
5、讲解例题:
例1:若一个角的补角等于它的余角4倍,求这个角的度数。
解: 设这个角是x °,则它的补角是( 180°-x°),余角是(90°-x°) 。
根据题意得:
(180-x°)= 4 (90-x°)
解之得: x =60
答:这个角的度数是60 °。
4、练习⑵:
 (1)图中给出的各角,那些互为补角?
(1)图中给出的各角,那些互为补角?
(2)填下列表:
|
∠a |
∠a的余角 |
∠a的补角 |
|
5° |
|
|
|
32° |
|
|
|
45° |
|
|
|
77° |
|
|
|
62°23′ |
|
|
|
x° |
|
|
结论:同一个锐角的补角比它的余角大90°。
(3)填空:
①70°的余角是 ,补角是 。
②∠a(∠a <90°)的它的余角是 ,它的补角是 。
重要提醒:ⅰ(如何表示一个角的余角和补角)
锐角∠a的余角是(90 °-∠ a )
∠a的补角是(180 °-∠ a )
ⅱ互余和互补是两个角的数量关系,与它们的位置无关。
3、探究互为补角的定义:
如果两个角的和是180°(平角),那么这两个角叫做互为补角,其中一个角是另一个角的补角。即:∠3是∠4的补角或∠4是∠3的补角。
2、练习⑴:
图中给出的各角,那些互为余角?
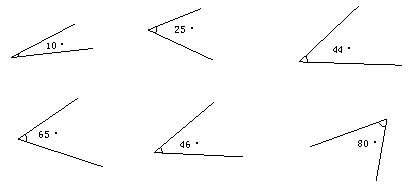
1、探究互为余角的定义:
如果两个角的和是90°(直角),那么这两个角叫做互为余角,其中一个角是另一个角的余角。即:∠1是∠2的余角或∠2是∠1的余角。
让学生观察意大利著名建筑比萨斜塔。
比萨斜塔建于1173年,工程曾间断了两次很长的时间,历经约二百年才完工。设计为垂直建造,但是在工程开始后不久便由于地基不均匀和土层松软而倾斜。
5、
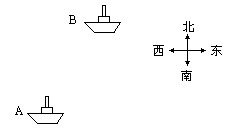
如图所示,A,B两条海上巡逻艇同时发现海面上有一不明物体,A艇发现该不明物体在它的东北方向,B艇发现该不明物体在它的南偏东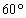 的方向上,请你试着在图中确定这个不明物体的位置.
的方向上,请你试着在图中确定这个不明物体的位置.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com