4.抛掷两枚骰子,两枚骰子的点数之积小于10的概率是多少?两枚骰子的点数之积为奇数的概率是多少?

3.在掷骰子的游戏中,当两枚骰子的点数之积为质数时,小明得2分;当两枚骰子的点数之积为6的倍数时,则小强得1分,你认为这个游戏对谁更有利?

2.小亮和小刚玩抛掷硬币的游戏,小刚手中拿有3枚硬币,同时抛掷这3枚硬币, 小明做记录,并规定:硬币落地后,若出现3个正面或3个反面,则小明得2分; 若出现2个正面1个反面,则小刚得1分;若出现2个反面1个正面,则两人均不得分,这个游戏公平吗?如果不公平,那么对谁更有利?如何修改规则可使游戏公平?

1.小明和小强玩抛掷硬币的游戏,每从手中持一枚硬币,两人同时抛掷硬币. 并规定:硬币落地后,出现两个正面朝上,则小明得2分,如果出现一枚正面朝上,一枚反面朝上,则小强得1分,这个游戏对两人公平吗?为什么?毛

4.3 游戏公平吗 同步练习

教师活动	学生活动	点　评
一、创设情境，引入新课 生活中，我们常常需要确定各种目标的位置。 (电脑显示课本第156页的第一幅图) 小丽现在位于中山路与北京路的十字路口，她想知道音乐喷泉在哪里。小明告诉她：音乐喷泉在中山北路西边50m，北京西路北边30m。按照小明的描述，小丽能找到音乐喷泉吗？怎样找呢？ 如果将北京(东、西)路和中山(南、北)路看成2条互相垂直的数轴，十字路口为它们的公共原点，那么中山北路西边50m可记为－50，北京西路北边30m可记为+30。 教师边讲解边电脑演示建立直角坐标系(在原图上)，你能在图上找出音乐喷泉的具体位置吗？ 电脑高亮显示音乐喷泉的位置。 师：音乐喷泉的位置就可以用一对实数　(－50，30)来描述。 提问：如果小明只告诉小丽“在中山北路西边50m”，小丽能找到音乐喷泉吗？只说“在北京西路北边30m”呢？ 二、讲解概念，合作探究 1．结合图形，讲解平面直角坐标系的概念 在这个图中，我们使用了两条数轴。请同学们观察一下，这两条数轴有何关系呢？ 根据学生回答，教师投影显示平面直角坐标系的概念。 (电脑高亮显示坐标轴、原点) 特别说明：通常，横轴取向右方向为正方向，纵轴取向上方向为正方向；两坐标轴上的单位长度通常是一致的。 2．动手操作，合作探究 (1)让学生画一个平面直角坐标系，要求单位长度为1厘米。 师巡视、指导学生画出平面直角坐标系。 (2)在直角坐标系中，由一对有序实数　(a，b)可以确定一个点P的位置。过x轴上表示实数a的点画x轴的垂线，过y轴上表示实数b的点画y轴的垂线，这两条垂线的交点，即为点P。 (师边讲解边电脑演示过程) 师：在前面的例子中，实际上就是由实数对　(－50，30)确定了表示音乐喷泉的点的位置。 提问： ①如果a的数值变化，b的数值不变，那么点P的位置会发生变化吗？ ②如果a的数值不变，b的数值变化，那么点P的位置会发生变化吗？ (3)提问：如果点Q是直角坐标系中一点，你能找到一对相应的有序实数吗？ 在学生回答交流的基础上总结：过点Q分别画x轴和y轴的垂线，如果垂足对应的实数分别是m、n，则点Q就可以用有序实数(m，n)来表示。 (师边总结边通过电脑演示过程) (4)归纳并引出坐标的概念 由此看来，在直角坐标系中一对有序实数可以确定一个点的位置；反之，任意一点的位置都可以用一对有序实数表示。这样的有序实数对叫做点的坐标。例如，点P的坐标为(a，b)，其中a称为点P的横坐标，b称为点P的纵坐标。 特别说明： ①横坐标应写在纵坐标的前面； ②点的坐标通常与表示该点的大写字母写在一起。 3．自解例题，总结规律 (1)出示例1题目，让学生尝试在自己所画出的直角坐标系中，描出题目中的点。 教师巡视，指导有困难的学生。 画完后，先同桌交流，再指名简述描出点A、E的过程。师电脑显示最终结果。 (2)引出象限的概念，并讨论各象限内及坐标轴上的点的坐标特点 师：为了便于研究，我们把2条坐标轴将平面分成的4个区域称为象限，按逆时针顺序分别记为第一、二、三、四象限。(电脑显示课本图4-7) 特别提醒：坐标轴上的点不属于任何象限。 提问： ①你能说出我们刚刚描出的各点所在的象限或坐标轴吗？ ②A、B、C、D四点分别位于四个象限，你能否根据它们的坐标并结合图形得到各象限内的点的坐标有什么特点吗？ 归纳板书： 第一象限(+，+)　第二象限(－，+) 第三象限(－，－)　第四象限(+，－) ③坐标轴上的点的坐标又有什么特点呢？ 归纳板书： 横轴上的点的纵坐标为0，纵轴上的点的横坐标为0。 (3)学生拿出课前发下去的印有例2的练习纸，让学生完成后，说出点A、B、C所在的象限及各自坐标。追问：与前面我们总结的规律一样吗？ 三、应用迁移，巩固提高 1．指出下列各点所在的象限或坐标轴。 点A(－8，－1)在　； 点B(3­－2，－32)在　； 点C(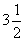，0)在　； 点A(π－3.14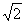，－1)在　。 2．已知点P(－3，4)，则点P到x轴的距离为　，到y轴的距离为　。 3．已知点A(x，y)且xy＝0，则点A在( ) A．原点 B．x轴上 C．y轴上 D．x轴上或y轴上 4．若点M(n，4－n)在第四象限，则( ) A．n＜0 B．n＞4 C．0＜n＜4 D．n＜0或n＞4 四、开展游戏，乐中促学 每位同学都表示平面内一点，让居中的横、纵向同学建立直角坐标系。先让学生说出自己表示的点所在的象限及坐标，然后让学生根据教师写出的坐标站起来。 五、课堂总结，拓展升华 1．通过本节课的学习，你有哪些收获？ 2．介绍笛卡尔创立直角坐标系的背景知识。 3．拓展：空间里的点怎样表示？ (学生回答后，电脑动画演示直线上的点、平面内的点、空间中的点的表示方法) 六、布置作业，练习巩固 第159页练习第1、2题； 第167页习题第2题。	观察图片，积极思考，回答问题。 　 　 　 观察平面直角坐标系的形成过程，领会实际模型中确定位置的方法。 　 　 　 学生思考，讨论。 　 　 　 积极思考，充分发表意见，自主揭示平面直角坐标系的构成与特点。 　 结合图形与教师的讲解，理解概念的实质内涵，掌握平面直角坐标系的绘制方法。 　 在教师指导下画平面直角坐标系。 　 　 通过教师的讲解及电脑演示，了解由一对有序实数确定点的位置的方法。 　 　 　 在教师的指导下讨论，总结。 　 　 　 通过积极探讨、教师的讲解及电脑演示，了解确定平面直角坐标系中点的坐标的方法。 　 在理解坐标概念的基础上，体会到“平面内的点与有序实数对是一一对应的”。 　 　 　 　 　 　 在已有的认知水平基础上进行实践尝试。 　 　 　 感悟象限的概念。 　 　 　 　 　 　 　 　 积极思考、大胆发表自己的见解，在讨论交流的基础上归纳得出结论。 　 　 　 　 　 　 自主完成例2，并借此验证上述结论的正确性。 　 　 完成练习。 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 积极参与游戏。 　 　 　 　 学生总结、倾听、猜想。	从生活事例出发创设情境，激发学生的学习欲望与兴趣。 　 充分挖掘现实生活的模型，通过直观感知让学生接受新的概念。 　 　 　 　 　 　 培养学生的观察和归纳能力。 　 　 　 　 　 　 　 让学生在画平面直角坐标系的过程中，深化对此概念的理解。 　 　 　 　 　 　 　 　 　 让学生充分感受和体验有序实数与点的位置的关系。 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 完成探究的过程，体会探究的乐趣和成功的喜悦。 　 　 　 　 　 　 　 　 　 　 通过练习深化对所学知识的感悟与理解。 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 通过游戏，寓教于乐。充分调动学生参与的积极性。 　 拓展学生的知识面，培养学生的发散思维和创新能力，激发学生勇于探索的热情。

兴化市沙沟石梁学校　严　骏

邮　　 编：　　　 225777

电　　 话：0523-5315269

多媒体课件。

探究式教学法。从学生的生活经验和已有的认知水平出发，提出问题，让学生通过合作交流，解决问题，掌握新知。

2．教学难点：

理解坐标平面内的点与有序实数对的一一对应关系。

1．教学重点：

使学生能正确画出平面直角坐标系，并能在给定的直角坐标系中，根据点的坐标描出点的位置，由点的位置写出它的坐标。