2．在解方程时，注意巧算；注意方程两根的取舍问题．

1．善于将实际问题转化为数学问题，严格审题，弄清各数据相互关系，正确布列方程．培养学生用数学的意识以及渗透转化和方程的思想方法．

例1、　某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元。为了扩大销售，增加盈利，商场决定采取适当的降价措施。经调查发现，在一定范围内，衬衫的单价每降一元，商场平均每天可多售出2件。如果商场通过销售这批衬衫每天要盈利1200元，衬衫的单价应降多少元？

例2、某商店经销一种销售成本为每千克40元的水产品，椐市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨1元，月销售量就减少10千克。针对这种水产品的销售情况，要使月销售利润达到8000元，销售单价应定为多少？

(月销售利润＝月销售量×销售单价－月销售成本．)

某商场从厂家以每件21元的价格购进一批商品，若每件的售价为a元，则可卖出(350-10a)件，商场计划要赚450元，则每件商品的售价为多少元？

5、如图，有长为24米的篱笆，一面利用墙(墙的最大可用长度为a为15米)，围成中间隔有一道篱笆的长方形花圃.

(1)如果要围成面积为45平方米的花圃，AB的长是多少米？

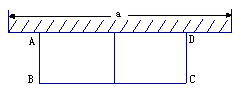(2)能围成面积比45平方米更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由.

4、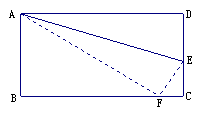如图，把长AD=10cm，宽AB=8cm的矩形沿着AE对折，使D点落在BC边的F点上，求DE的长.

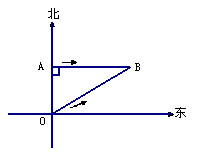
3、如图所示，人民海关缉私巡逻艇在东海海域执行巡逻任务时，发现在其所处的位置O点的正北方向10海里外的A点有一涉嫌走私船只正以24海里/时的速度向正东方向航行，为迅速实施检查，巡逻艇调整好航向，以26海里/时的速度追赶.在涉嫌船只不改变航向和航速的前提下，问需要几小时才能追上(点B为追上时的位置)？

2、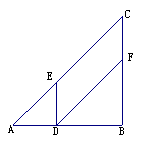如图，在Rt△ABC中，AB=BC=12cm，点D从点A开始沿边AB以2cm/s的速度向点B移动，移动过程中始终保持DE∥BC，DF∥AC，问点D出发几秒后四边形DFCE的面积为20cm²？

1、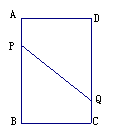如图，A、B、C、D为矩形的四个顶点，AB=16cm，BC=6cm，动点P、Q分别从点A、C出发，点P以3cm/s的速度向点B移动，一直到达B为止；点Q以2cm/s的速度向点D移动.经过多长时间P、Q两点之间的距离是10cm？

2、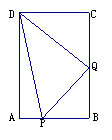如图，在矩形ABCD中，AB=6 cm，BC=12 cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动，问几秒后△PBQ的面积等于8 cm²？

解：