
1. 重点:角的第二定义,角大小的比较方法。
3. 在操作活动中认识角的平分线,能画出一个角的平分线。
2. 会比较角的大小,能估计一个角的大小。
1. 在现实情境中,进一步丰富对角与锐角,钝角,直角,平角,周角及其大小关系的认识。
4.5角的大小比较同步练习
第1题. 一个角的补角的 等于它的余角,则这个角是 度.
等于它的余角,则这个角是 度.
第2题. 一个角的补角加上14°,等于这个角的余角的5倍,这个角的度数是 .
第3题. 如果两个角互补,并且它们的差是30°,那么较大的角是 °.
第4题. 若 ,
, ,那么
,那么 ,理由是 .
,理由是 .
第5题. 已知: ,且
,且 ,求
,求 和
和 .
.
第6题. 如图,点 是直线
是直线 上的点,
上的点, ,
, ,
, 三个角从小到大依次相差25°,则这三个角的度数是 .
三个角从小到大依次相差25°,则这三个角的度数是 .


第7题. 如图, ,
, ,则
,则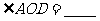 .
.


第8题. 某火车站的钟楼上装有一电子报时钟,在钟面的边界上每一分钟的刻度处都装有一只小彩灯,晚上九点三十五分二十秒时,时针与分针所夹的角 内装有 只小彩灯.
内装有 只小彩灯.
第9题. 如图, 是直线
是直线 上的点,
上的点, 是
是 的平分线,
的平分线, 是
是 的平分线,求
的平分线,求 的度数.
的度数.


⑴一变:如图, ,
, 平分
平分 ,问
,问 是否平分
是否平分 ?
?
⑵二变:如图,点 在直线
在直线 上,且
上,且 ,
, 平分
平分 ,
, ,下面四个结论,错误的有( )
,下面四个结论,错误的有( )
①图中必有3个钝角; ②图中只有3对既相邻又互补的角;
③图中没有45°的角; ④ 是
是 的平分线.
的平分线.
A.0个 B.1个 C.2个 D.3个
第10题. 已知 ,
, 是
是 的平分线,则
的平分线,则 的余角等于 .
的余角等于 .
.
第11题. 如图, ,
, ,
, ,
, 平分
平分 ,求
,求 的度数.
的度数.


第12题. 若把一个平角三等分,则两旁的两个角的平分线所组成的角等于( )
A. 平角 B.
平角 B. 平角 C.
平角 C. 平角 D.
平角 D.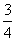 平角
平角
第13题. 已知 和
和 之和为
之和为 ,这两个角的平分线所成的角( )
,这两个角的平分线所成的角( )
A.一定是直角 B.一定是锐角 C.一定是钝角 D.是直角或锐角
第14题. 如图, 是直线
是直线 上一点,
上一点, ,
, ,
, 平分
平分 ,则图中和为
,则图中和为 的两个角有( )
的两个角有( )
A.3对 B.4对 C.5对 D.6对


第15题. 已知: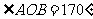 ,
, ,
, ,求
,求 的大小.
的大小.
第16题. 互余且相等的两个角都是 °.
第17题. 一个锐角的补角比这个角的余角大 °.
第18题. 如图,已知 ,
, 平分
平分 ,且
,且 ,求
,求 的度数.
的度数.


第19题. 下列说法中错误的个数是 ( )
①线段有两个端点,直线有一个端点; ②角的大小与我们画出的角的两边的长短无关;③线段上有无数个点; ④同角或等角的补角相等; ⑤两锐角的和一定大于直角.
A.1个 B.2个 C.3个 D.4个
第20题. 如图,平原上有 ,
,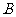 ,
, ,
, 四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
⑴不考虑其他因素,请你画图确定蓄水池 点的位置,使它与四个村庄的距离之和最小.
点的位置,使它与四个村庄的距离之和最小.
⑵计划把河中的水引入蓄水池 中,怎样开的渠最短?并说明根据.
中,怎样开的渠最短?并说明根据.


第21题. 下列说法中正确的是( )
A.一条射线把一个角分成两个角,这条射线是这个角的角平分线
B.点到直线的距离是指从直线外一点到这条直线的垂线的长度
C.若 ,则点
,则点 是线段
是线段 的中点
的中点
D.有 ,
, ,则点
,则点 在线段
在线段 上,点
上,点 在线段
在线段 外
外
第22题. 已知线段 ,在
,在 的延长线上取一点
的延长线上取一点 ,使
,使 ,在
,在 的反向延长线上取一点
的反向延长线上取一点 ,使
,使 ,那么线段
,那么线段 是线段
是线段 的 ( )
的 ( )
A. B.
B. C.
C. D.
D.
第23题. 已知∠α与∠β互余,且∠α=40°,则∠β的补角为 度.
第24题. 请你用三角板、圆规或量角器等工具,画∠POQ=60°,在它的边OP上截取OA=50 mm,OQ上截取OB=70 mm,连结AB,画∠AOB的平分线与AB交于点C,并量出AC和OC 的长.(结果精确到1 mm,不要求写作法).
第25题. 已知 ,那么它的补角等于
,那么它的补角等于  .
.
第26题. 图中给出的各角中,哪些互为余角?哪些互为补角?


小结:制作立体图形――先转化为平面图形(平面展开图),再转化为立体图形(折叠).
作业:
(1)自己设计制作一个正六棱柱形状(底面是6条边相等、6个角都相等的六边形,6个侧面都是长方形)的包装盒;
(2)自己设计制作一个圆柱形的包装纸盒.
4.评价、小结
评价各组的活动情况,小结活动的主要收获.
3.交流、比较
各组展示本组的作品,并介绍设计思想和制作过程.
讨论本组的作品,重点探究以下问题:
(1)制成的包装盒是否是长方体?若不是,是哪个地方出项了问题?如何改正?
(2)从使用性上看,包装盒形状、尺寸是否合理?用料是否节省?是否需要改进?
(3)包装盒的外观设计是否美观?
(4)对平面图形与立体图形的联系有哪些新认识?
2.设计制作
(1)先在一张软纸上画出包装盒表面展开图的草图,简单设计一下,裁纸、折叠,观察效果.如果发生问题,调整原来的设计,知道达到满意的初步设计.
(2)在硬纸板上,按照初步设计,画好包装盒的表面展开图,注意要预留出粘合处,并要减去适当的棱角.在表面展开图上进行图案与文字的美术设计.
(3)裁下表面展开图、折叠并粘好粘合处,得到长方体包装盒


活动步骤:
1.观察、讨论
以5-6人为一组,各组确定所要设计制作的包装盒的类别,明确分工.
(1)观察作为参考物的包装盒,分析其各面、各棱的大小与位置关系.
(2)拆开盒子,把它铺平,得到表面展开图;观察它的形状,找出对应长方体各面的相应部分;度量各部分的尺寸,找出其中的相等关系.
(3)把表面展开图复原为包装盒,观察它是如何折叠并粘到一起的.
(4)多拆、装几个包装盒,注意它们的共同特征.
(5)经过讨论,确定本组的设计方案.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com