1.如图1所示,下列说法不正确的是(　 )毛

　　 A.点B到AC的垂线段是线段AB;　 B.点C到AB的垂线段是线段AC

C.线段AD是点D到BC的垂线段;　 D.线段BD是点B到AD的垂线段

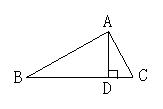
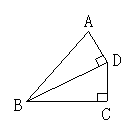
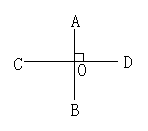
　　　　 (1)　　　　　　　　　　 (2)　　　　　　　　　 　(3)

2．探索活动

　　 活动一：

　　 展示一幅列车行驶或车厢内的图片．用下列问题引导学生加入小明、小丽、小亮和小华的讨论，感受常量与变量的意义：

　　 (1)列车在行驶，位置在改变，因此与位置有关的数量在改变，这里有不变的数量吗?

　　 (2)除了小丽、小明所说的那些不变的数量外，在这个问题中还有不变的数量吗?

　　 (3)除了小亮、小华所说的那些变化的数量外，在这个问题中还有变化的数量吗?

　　 活动二：

　　 可以用下列问题引导学生展开活动，体会函数的意义：

　　 (1)你从水库工作人员制作的表格里获得哪些信息?水位高低与水库容量有什么关系?

　　 (2)小鱼的条数n与所需火柴棒的根数S的关系为S＝8+6(n-1)，说说你从中获得的信息；

　　 (3)变化中的圆面积与半径的大小密切相关，你能大致描述它们之间的关系吗?

　 (4)上述问题有共同之处吗?说说你的看法．

1．情境创设

　　 情境一：

　　 在行驶的列车上，围绕位置变化与数量变化的话题，谈论车速、路程、时间的变化，是学生熟悉的场景，能自然贴切地引入常量与变量的概念。如果学生没有乘坐火车的经历，可改用汽车或创设其他类似情境．

　　 情境二：

　　 分别用表格、关系式和语言等方式给出不同的实际问题，让学生从这些情境中，发现在各种变化过程中，往往存在着两个相互联系的变量，从而引入函数的概念．

4．能根据实际问题的意义以及函数关系式，确定函数的自变量取值范围，并会求出函数值．

[教学过程(第一课时)]

3．能根据图象对简单实际问题中的函数关系进行分析．

2．通过实例，了解函数的概念和表示方法，并能说出一些函数的实例．

1．通过简单实例，了解常量与变量的意义．

5．1　函数

[教学目标]

2．探索活动

　　 活动一：

　　 展示一幅列车行驶或车厢内的图片．用下列问题引导学生加入小明、小丽、小亮和小华的讨论，感受常量与变量的意义：

　　 (1)列车在行驶，位置在改变，因此与位置有关的数量在改变，这里有不变的数量吗?

　　 (2)除了小丽、小明所说的那些不变的数量外，在这个问题中还有不变的数量吗?

　　 (3)除了小亮、小华所说的那些变化的数量外，在这个问题中还有变化的数量吗?

　　 活动二：

　　 可以用下列问题引导学生展开活动，体会函数的意义：

　　 (1)你从水库工作人员制作的表格里获得哪些信息?水位高低与水库容量有什么关系?

　　 (2)小鱼的条数n与所需火柴棒的根数S的关系为S＝8+6(n-1)，说说你从中获得的信息；

　　 (3)变化中的圆面积与半径的大小密切相关，你能大致描述它们之间的关系吗?

　 (4)上述问题有共同之处吗?说说你的看法．

1．情境创设

　　 情境一：

　　 在行驶的列车上，围绕位置变化与数量变化的话题，谈论车速、路程、时间的变化，是学生熟悉的场景，能自然贴切地引入常量与变量的概念。如果学生没有乘坐火车的经历，可改用汽车或创设其他类似情境．

　　 情境二：

　　 分别用表格、关系式和语言等方式给出不同的实际问题，让学生从这些情境中，发现在各种变化过程中，往往存在着两个相互联系的变量，从而引入函数的概念．